Feladat: Gy.1747 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Ács J. ,  Bacsur K. ,  Bereznai M. ,  Bölcsföldi L. ,  Cselők L. ,  Danyi P. ,  Elek G. ,  Fodor L. ,  Gáti Zs. ,  Jordán J. ,  Juhász 665 I. ,  Karakas J. ,  Keszei Zs. ,  Kiss 352 Gy. ,  Ligeti R. ,  Lőrinczi Zsuzsanna ,  Seres I. ,  Simonyi G. ,  Tésik P. ,  Tóth 555 T. ,  Valet B. ,  Várnagy Katalin 
Füzet: 1978/november, 138 - 140. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Pont körüli forgatás, Körülírt kör, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):Feladatok: 1978/február: Gy.1747

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha adott két pont, K és L, és egy 0<α<180∘ szög, akkor azoknak az M pontoknak a mértani helye, amelyekből a KL szakasz α szög alatt látszik, két körív; amelyek a KL egyenesre nézve szimmetrikusan helyezkednek el. Ebben a jól ismert állításban a látószög az M-ből K-ba, illetve L-be futó félegyenesek közti szög, ekkora forgatás viszi át az egyik félegyenest a másikba.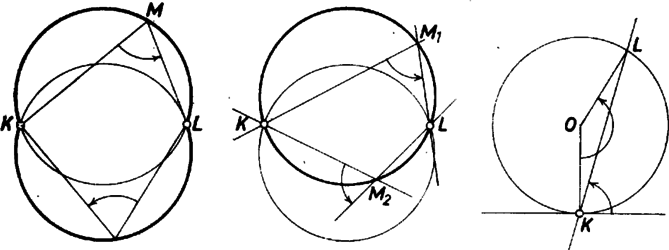

 
 

Ha a forgatás irányát is megadjuk, tehát megmondjuk, hogy az az óramutató járásával megegyező, vagy ellentétes irányú legyen, akkor a két körív közül már csak az egyik felel meg, hiszen a tükrözés megfordítja a forgásirányt. (Azt, hogy az ugyanahhoz a körívhez tartozó pontokhoz egyenlő forgásirányok is tartoznak, a látókörök egyenlőségére vonatkozó szokásos bizonyítással láthatjuk be, csak most közben a forgásirányra is ügyelni kell.)
Az adott α látószöghöz tartozó köríveket tartó körök másik ívén a látószög 180-α. Ha nem az M-ből induló MK, ML félegyenesek szögét kérdezzük, hanem azt az óramutató járásával ellentétes irányú (azaz pozitív) forgást, ami az MK egyenest az ML egyenesbe viszi, ez már az egész kör mentén ugyanaz lesz. Hiszen ha úgy választjuk az íveken felvett M1, M2 pontok betűzését, hogy az M1, K, M2, L körüljárás legyen pozitív irányú a körön, akkor M1KM2L konvex négyszög, melyben a KM1L belső szög egyenlő az M2-nél levő külső szöggel.
Beilleszthetők a két látókörívet tartalmazó körön a körívek pontjai közé maguk a K, L pontok is, ha M=K esetén az MK egyenes alatt e kör K-beli érintőjét, M=L esetén pedig ML-en az L-beli érintőt értjük. Most azt könnyebb először igazolni, hogy például a K-beli érintőt a KL egyenesbe vivő pozitív irányú forgatás kétszerese az OK félegyenest OL-be viszi. Ennek alapján a kerületi és középponti szögek közti összefüggés segítségével bizonyíthatjuk állításunkat. (Tulajdonképpen célszerű az egész tételsor bizonyítását ezzel kezdeni, és erre vezetni vissza az általános esetet is.)
Most térjünk rá a feladat állításának bizonyítására. Ha az AP egyenest γ nagyságú pozitív irányú forgatás viszi át a BP egyenesbe, akkor az A, B, P pontokon átmenő kör AB egyenesre vonatkozó kC tükörképe azon Q pontok mértani helye, amelyek mellett az AQ egyenest γ nagyságú negatív irányú forgatás viszi át a BQ egyenesbe. Hasonlóan kapjuk, hogy ha a BP egyenest α nagyságú pozitív irányú forgatás viszi át a CP egyenesbe, akkor a BCP háromszög köré írt kör BC-re vonatkozó kA tükörképe azon R pontok mértani helye, amelyek mellett a BR egyenest α nagyságú negatív irányú forgatás viszi át a CR egyenesbe.
Ha van a kA, kC köröknek B-től különböző közös pontja, mondjuk S, akkor arra egyrészt az teljesül, hogy az SA egyenest SB-be γ nagyságú negatív irányú forgatás viszi át, másrészt az, hogy SB-t SC-be α nagyságú negatív irányú forgatás. Tehát SA-t SC-be (α+γ) nagyságú negatív irányú forgatás viszi át (ami helyett α+γ>180∘ esetén az α+γ-180∘ szöget vehetjük, hiszen a 180∘-os forgatás az SA egyenest önmagába viszi át). Így S rajta van az ACP háromszög köré írt kör AC-re vonatkozó tükörképén, hiszen AP-t BP-be, majd BP-t CP-be pozitív irányban forgatva éppen az AP-t CP-be vivő pozitív irányú forgatást hajtjuk végre (esetleg még egy felesleges 180∘-os forgatást is). Tehát a három körnek van közös pontja.
Akkor is van a három körnek közös pontja, ha kA és kC érinti egymást B-ben, hiszen akkor a B-beli érintőjük közös. Emiatt a BA egyenest negatív irányban γ szöggel elforgatva e közös érintőt kapjuk, amit α szöggel tovább forgatva a BC egyenesbe jutunk. Tehát most B maga van rajta a kB körön. (Ez a helyzet akkor fordul elő, ha P-t az ABC háromszög köré írható k kör AC-re vonatkozó tükörképén vesszük fel.)
Eddig hallgatólagosan feltételeztük, hogy P nincs az AB, BC, CA egyenesek egyikén sem, különben a három kör valamelyike nem létezik. Átvihető az állításunk erre az esetre is, ha egy egyenesbe eső három pont esetén a rajtuk átmenő kör helyett közös egyenesüket vesszük, csak azt kell kizárnunk, hogy P valamelyik csúccsal legyen azonos. A bizonyításban ez csak annyi módosítást igényel, hogy azt is megengedjük, hogy a forgatás az egyeneseket helyükön hagyja.