Kezdőlap


Feladat:	Gy.1740	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ács J. , Arató M. , Bakó I. , Bareith A. , Beleznay F. , Benkő B. , Bereznai M. , Bölcsföldi L. , Csiki A. , Csillag Zs. , Czifra A. , Danyi P. , Elek G. , Fábián T. , Gulyás A. , Horváth 165 T. , János Ágnes , Jordán J. , Juhász 665 I. , Junger Éva , Kámán L. , Kántor Zs. , Kardos J. , Kassai J. , Kasza A. , Kiss 352 Gy. , Kovács 134 I. , Krausz F. , Lévai P. , Lipusz Cs. , Madi T. , Magyar G. , Nagy Edina , Pekó Éva , Pöltl J. T. , Pöstyéni F. , Seres I. , Süvegh K. , Szabó 457 L. , Tóth 555 T. , Umann G. , Vértesi L.
Füzet:	1978/május, 210. oldal		PDF \| MathML
Témakör(ök):	Térfogat, Poliéderek súlypontja, Tetraéderek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1978/január: Gy.1740

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a tetraéder csúcsait $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4}$ -gyel, súlypontját $S$ -sel, az $A_{1} A_{3}$ él felezőpontját $F_{13}$ -mal, az $A_{2} A_{4}$ él felezőpontját $F_{24}$ -gyel. Mint ismeretes, a tetraéder súlyvonalának nevezzük a tetraéder csúcsait a szemközti háromszöglap súlypontjával összekötő egyeneseket. Azt is tudjuk, hogy a tetraéder súlyvonalai egymást a laphoz közelebb eső negyedelőpontjukban metszik, ezt nevezzük a tetraéder súlypontjának. (L. II. o. tankönyv 154. oldal.)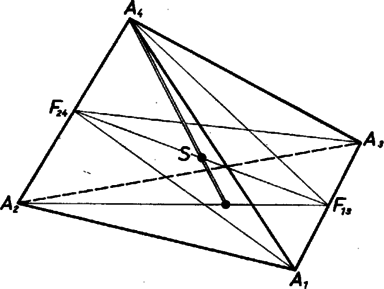

A továbbiakban azt fogjuk igazolni, hogy az általunk felvett síkok mindegyike átmegy a tetraéder súlypontján.
Tekintsük pl. az

A_{2}

A_{4}

F_{13}

, valamint az

A_{1}

A_{3}

F_{24}

pontokon átmenő síkokat. Mivel

A_{1} A_{3}

és

A_{2} A_{4}

egyenesek nincsenek egy síkban, azért a síkok nem esnek egybe, tehát van metszésvonaluk, s ez éppen az

F_{13}

F_{24}

pontokon átmenő egyenes. Az

A_{2} A_{4} F_{13}

sík és az

A_{1} A_{3} F_{24}

sík mindegyike tartalmazza a tetraéder súlypontját, így

S

a két sík metszésvonalán van; ezzel igazoltuk állításunkat.
Ha a tetraéder súlypontját összekötjük a csúcsaival, az így kapott

4

kis tetraéder térfogata az eredeti térfogat

1 / 4

része lesz, mivel alaplapja egy tetraéderlap, és magassága a tetraéder megfelelő magasságának

1 / 4

-e. A feladatban szereplő síkok további 6‐6 részre osztják ezeket a kis tetraédereket, mivel a síkok átmennek a tetraéder súlypontján és mindegyikük a tetraéder két-két lapját egy-egy súlyvonalban metszi. Így összesen

6 \times 4 = 24

rész keletkezik. A részek térfogatai mind egyenlők, mert a háromszöget a súlyvonalai 6 egyenlő területű részre osztják, s ezek lesznek a kis tetraéderek alapjai. Így tehát egy rész térfogata a tetraéder térfogatának

1 / 24

-ed része.