Feladat: Gy.1739 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bajnok B. ,  Cseri I. ,  Czifra A. ,  Elter J. ,  Gát Gy. ,  Gyúró E. ,  Hochenburger R. ,  Horváth 158 A. ,  Horváth Á. ,  Kántor Zs. ,  Kiss 352 Gy. ,  Korondi P. ,  Kovács 764 Z. ,  Márkus L. ,  Németh R. ,  Pátkai Andrea ,  Pintér 359 F. ,  Ruisz T. ,  Seres I. ,  Umann G. ,  Varga J. ,  Vértesi L. ,  Vértessy Bea ,  Winkler R. 
Füzet: 1978/május, 209 - 210. oldal  PDF  |  MathML 
Témakör(ök): Trigonometrikus egyenletrendszerek, Rombuszok, Vektorok felbontása összetevőkre, Helyvektorok, Gyakorlat
Hivatkozás(ok):Feladatok: 1978/január: Gy.1739

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat állítása csak akkor igaz, ha |α-β|≠180∘. Először e kiegészítő feltétel mellett bizonyítjuk állításunkat, majd megvizsgáljuk az |α-β|=180∘ e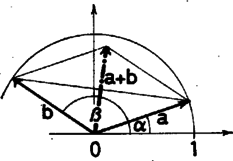setet.

 
 

Vegyük fel a koordinátarendszerben az a és b egységvektorokat, amelyeknek kezdőpontjuk az origó és irányszögük α, ill. β. Az egységvektorok koordinátái a(cosα,sinα), b(cosβ,sinβ). Képezzük az a+b összegvektort, a vektorok összeadási szabálya szerint az összegvektor az egységnyi oldalhosszúságú rombusznak az origóból kiinduló átlója, melynek koordinátái (cosα+cosβ,sinα+sinβ).
Fordítva, ha ismerjük az a+b vektor koordinátáit, akkor meg tudjuk szerkeszteni az összegvektort, és mivel a rombusz átlói merőlegesen felezik egymást, az |a+b| hosszúságú szakasz felezőmerőlegese kimetszi az egységsugarú körből az a és b egységvektorok végpontjait, kivéve egy esetet, ha a+b=0; erre még visszatérünk. Ez azt jelenti, hogy a sinα+sinβ és cosα+cosβ összefüggések egyértelműen meghatározzák az α-t és β-t, tehát (1) valóban csak úgy teljesülhet, ha x=α és y=β, vagy x=β és y=α.
Most térjünk vissza arra az esetre, amikor a+b=0. Ez akkor áll fenn, ha |α-β|=180∘, s ekkor minden olyan x, y szögpár megoldás, amelyre |x-y|=180∘.
 

Megjegyzések. 1. A feladatot meg lehet oldani trigonometrikus összefüggések felhasználásával is. A kiegészítő feltételre akkor is szükség van.
2. Többen észrevették, hogy az állítás így nem igaz, s erre ellenpéldát adtak. Az ő megoldásukat is helyesnek fogadtuk el.