Kezdőlap


Feladat:	Gy.1733	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1978/április, 165 - 166. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Beírt kör, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1977/december: Gy.1733

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C$ háromszög körülírt körének középpontját $O$ -val, $O$ -nak az $a$ , $b$ , $c$ oldalaktól való távolságát rendre $d_{a}$ , $d_{b}$ , $d_{c}$ -vel, a beírt kör sugarát $r$ -rel. Választhatjuk a jelölést úgy, hogy $a b \geq c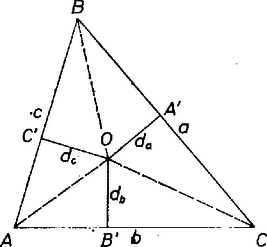$ legyen.

Azt kell bizonyítani, hogy

\begin{matrix} d_{a} + d_{b} + d_{c} \geq 3 r . \end{matrix}

Írjuk fel az

A B C

háromszög területének,

t

-nek kétszeresét kétféleképpen:

\begin{matrix} 2 t = 2 r s = r (a + b + c), \end{matrix}

(1)

másrészt

\begin{matrix} 2 t = a d_{a} + b d_{b} + c d_{c} . \end{matrix}

(2)

Ez utóbbi egyenlőség helyes, mivel a feltétel szerint a háromszög hegyesszögű, és így

O

a belsejében van.
A

d_{a}

d_{b}

d_{c}

szakaszoknak a megfelelő oldalakkal való metszéspontjait jelöljük

A'

B'

C'

-vel. Az

O A B'

C O A'

B O C'

háromszögekből

\begin{matrix} d_{b}^{2} + {(\frac{b}{2})}^{2} = d_{a}^{2} + {(\frac{a}{2})}^{2} = d_{c}^{2} + {(\frac{c}{2})}^{2} = r^{2}, \end{matrix}

s mivel

a \geq b \geq c

, innen

d_{a} \leq d_{b} \leq d_{c}

adódik. Az

(a - b) (d_{a} - d_{b})

szorzat tehát biztosan negatív vagy 0. A szorzást elvégezve, s a másik két oldalra is felírva az egyenlőtlenségeket, kapjuk

\begin{matrix} a d_{a} + b d_{b} \leq b d_{a} + a d_{b}, \\ b d_{b} + c d_{c} \leq c d_{b} + b d_{c}, & (3) \\ a d_{a} + c d_{c} \leq c d_{a} + a d_{c} . \end{matrix}

Az egyenlőtlenségek megfelelő oldalait összeadva és mindkét oldalhoz hozzáadva még (2) jobb oldalát

\begin{matrix} 3 (a d_{a} + b d_{b} + c d_{c}) \leq (a + b + c) (d_{a} + d_{b} + d_{c}) . \end{matrix}

(2) szerint a bal oldalon

6 t

áll, ami (1) szerint egyenlő

3 r (a + b + c)

-vel, azaz

\begin{matrix} 3 r (a + b + c) \leq (a + b + c) (d_{a} + d_{b} + d_{c}) . \end{matrix}

Végigosztva az

(a + b + c) > 0

-val, éppen a bizonyítandó egyenlőtlenséget kapjuk.