Kezdőlap


Feladat:	Gy.1714	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1978/szeptember, 12 - 14. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Beírt kör, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1977/október: Gy.1714

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a körülírt $k$ kör sugarát $R$ -rel, a beírt $k_{1}$ kör sugarát $r$ -rel, és az adott szöget 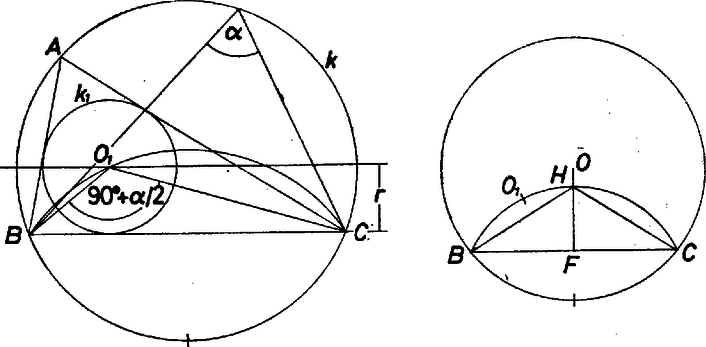$α$ -val.
A szerkesztés során felhasználjuk, hogy $R$ és $α$ egyértelműen meghatározza a háromszög $a$ oldalát.

Vegyük fel a

k

kört, rajzoljuk bele az

α

szöget, ezzel megkaptuk a keresett háromszög

B

és

C

csúcsát. A

k_{1}

kör

r

sugara ismeretében keressük középpontjának mértani helyét. Ez egyrészt a

B C

egyenestől

r

távolságban húzott párhuzamos egyenesen, másrészt a

B C

szakasz fölé írt

90^{\circ} + \frac{α}{2}

szögi látóköríven van. A

B C

szakasz a

k

kört két részre osztja,

α

a két körív valamelyikéhez tartozik, aszerint, hogy hegyesszög vagy tompaszög. A beírt kör középpontját a

B C

szakasz ugyanazon oldalán kell keresnünk, amelyiken az

α

is fekszik. A két mértani hely közös pontja (amennyiben létezik) megadja

k_{1}

középpontját. Megrajzoljuk

k_{1}

-et, majd

B

és

C

pontokból érintőt szerkesztünk

k_{1}

-hez, ezek metszik ki

k

-ból az

A

csúcsot.
Az így kapott háromszög nyilván eleget tesz a feltételnek, csupán azt kell belátnunk, hogy az érintők metszéspontja rajta van a

k

körön. Jelöljük a

k_{1}

kör középpontját

O_{1}

-gyel.

B O_{1}

és

C O_{1}

A B C

háromszögben szögfelezők, így

\begin{matrix} B A C ∢ = 180^{\circ} - (A B C ∢ + A C B ∢) = 180^{\circ} - 2 (O_{1} B C ∢ + O_{1} C B ∢) = 180^{\circ} - \\ - 2 (180^{\circ} - (90^{\circ} + \frac{α}{2})) = α . \end{matrix}

Tehát

C

valóban a

B C

szakaszhoz és

α

szöghöz tartozó látóköríven van.
Ha a feladatnak van megoldása, akkor általában kettő van, s ezek a

B C

felezőmerőlegesre szimmetrikusak. Egy megoldás van, ha a látókörív éppen érinti a párhuzamost, és nincs megoldás, ha nincs közös pontjuk.
Vizsgáljuk meg a megoldhatóság feltételét. Nyilván

0^{\circ} < α < 180^{\circ}

és

R ≧ 2 r

mellett jöhet létre csak háromszög. Jelöljük

B C

felezőpontját

F

-vel, a

k

középpontját

O

-val,

O F

-nek a látókörívvel való metszéspontját

H

-val.
Ekkor

\begin{matrix} F C = \frac{B C}{2} = R sin α, \\ F H = \frac{B C}{2} \cdot tg(45^{\circ}+\frac{α}{4}) \end{matrix}

és mivel

r ≦ F H ≦ R sin α tg(45^{\circ}+\frac{α}{4}) = 2Rsin\frac{α}{2}(1 +sin\frac{α}{2})

II. megoldás. Induljunk ki az

α

szögből, és szárai közé szerkesszük meg az

r

sugarú

k_{1}

beírt kört. Mivel az

α

-val szemközti oldal hossza a

k

körülírt kör

R

sugarával adott, ehhez a körhöz kell adott hosszúságú érintőt szerkeszteni.
Gondoljuk a feladatot megoldottnak, és rajzoljuk meg a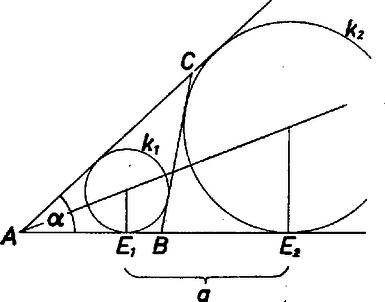

B C

oldal külső érintő körét,

k_{2}

-t. Érintse az

A B

egyenest a

k_{1}

kör

E_{1}

-ben, a

k_{2}

E_{2}

-ben. Ismeretes, hogy

A E_{2} = s

(ahol

s

a háromszög félkerülete)

A E_{1} = (s - a)

, ahonnan

\begin{matrix} A E_{2} - A E_{1} = s - (s - a) = a . \end{matrix}

A szerkesztést ezután úgy végezhetjük el, hogy az

E_{1}

ponttól továbbhaladva az

A E_{1}

félegyenesen felmérjük az

E_{1} E_{2} = a

távolságot. Megrajzoljuk az

E_{2}

-ben érintő

k_{2}

kört, majd

k_{1}

k_{2}

körökhöz közös belső érintőt szerkesztünk. A feladat megoldásainak száma

2

1

vagy

0

, aszerint, hogy a

k_{1}

k_{2}

köröknek nincs közös pontjuk, érintik egymást, vagy két közös pontjuk van.
Könnyű belátni, hogy az így kapott háromszög eleget tesz a feltételnek.