Kezdőlap


Feladat:	Gy.1710	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Nagy Gábor
Füzet:	1978/február, 70 - 71. oldal		PDF \| MathML
Témakör(ök):	Nevezetes azonosságok, Egyenlőtlenségek grafikus megoldása, Irracionális egyenlőtlenségek, Derékszögű háromszögek geometriája, Körülírt kör, Súlypont, Kör egyenlete, Jensen-féle egyenlőtlenség, Gyakorlat
Hivatkozás(ok):	Feladatok: 1977/október: Gy.1710

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mérjünk fel két merőleges félegyenesre a közös $O$ kezdőpontjukból kiindulva $c$ , $b$ , $a$ , illetve $\sqrt[]{1 - a^{2}}$ , $\sqrt[]{1 - b^{2}}$ és $\sqrt[]{1 - c^{2}}$ hosszúságú szakaszokat, és jelöljük a kapott végpontokat $A$ -val, $B$ -vel. Az $A$ és $B$ végpontokat egy $3$ egység hosszú töröttvonal köti össze, ezért $A B = d \leq 3$ . A Pitagorasz-tételt felhasználva adódik, hogy

\begin{matrix} \bar{O B} = \sqrt[]{1 - a^{2}} + \sqrt[]{1 - b^{2}} + \sqrt[]{1 - c^{2}} = \sqrt[]{d^{2} - {(a + b + c)}^{2}} \leq \sqrt[]{9 - {(a + b + c)}^{2}} . \end{matrix}

Az egyenlőség akkor és csak akkor állhat fenn, ha

d = 3

, azaz

a = b = c

Nagy Gábor (Székesfehérvár, Teleki B. Gimn., III. o. t.)

II. megoldás. Mivel az

(1)

egyenlőtlenség mindkét oldalán nem negatív kifejezések állnak, ezért négyzetre emelés és rendezés után vele ekvivalens egyenlőtlenséget kapunk: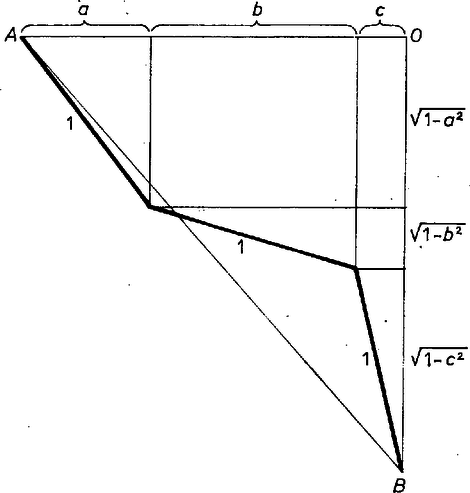

\begin{matrix} \sqrt[]{(1 - a^{2}) (1 - b^{2})} + \sqrt[]{(1 - a^{2}) (1 - c^{2})} + \sqrt[]{(1 - b^{2}) (1 - c^{2})} \leq 3 - a b - a c - b c . (2) \end{matrix}

Elég azt megmutatni, hogy az alábbi egyenlőtlenség teljesül

\begin{matrix} \sqrt[]{(1 - x^{2}) (1 - y^{2})} \leq 1 - x y, \end{matrix}

(3)

hiszen itt az

x

és

y

helyére rendre az

a, b

;

a, c

;

b, c

számpárokat helyettesítve és az egyenlőtlenségeket összeadva a bizonyítandó állításhoz jutunk.
A

(3)

egyenlőtlenség igazolása pl. újabb négyzetre emeléssel történhet. Négyzetre emelés és rendezés után ugyanis az

{(x - y)}^{2} \geq 0

adódik, amiből az is kiolvasható, hogy az eredeti egyenlőség akkor és csak akkor teljesül, ha

a = b = c

III. megoldás. Tekintsük az

f (x) = \sqrt[]{1 - x^{2}}

függvényt. Ennek képe egy origó középpontú egységsugarú félkör. Válasszunk ezen a félkörön három pontot. Ha a pontok első koordinátája

a

b

c

, akkor a megfelelő második koordináták rendre

\sqrt[]{1 - a^{2}}

\sqrt[]{1 - b^{2}}

és

\sqrt[]{1 - c^{2}}

. A három pont által meghatározott háromszög súlypontjának koordinátái:

\begin{matrix} x_{S} = \frac{a + b + c}{3}, y_{S} = \frac{\sqrt[]{1 - a^{2}} + \sqrt[]{1 - b^{2}} + \sqrt[]{1 - c^{2}}}{3} . \end{matrix}

Mivel a háromszög súlypontja a körülírt kör belsejében van, ezért

y_{S} \leq f (x_{S})

. Ezt az egyenlőtlenséget

3

-mal szorozva a bizonyítandó egyenlőtlenséget kapjuk.

Megjegyzés. A III. megoldásban felhasznált gondolat nagyon sok egyenlőtlenség igazolására használható. Az érdeklődők Jensen-egyenlőtlenség néven olvashatnak róla pl. Molnár Emil: Matematikai versenyfeladatok gyűjteménye című könyvében.