Kezdőlap


Feladat:	Gy.1708	Korcsoport: 14-15	Nehézségi fok: nehéz
Füzet:	1978/január, 20. oldal		PDF \| MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Mértani helyek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1977/szeptember: Gy.1708

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel az $A A_{1}$ , $B B_{1}$ húrok metszik egymást, $A B$ -nek ugyanazon az oldalán vannak, $M$ az ezen az oldalon levő félkör belső pontja, és a félköríven az említett pontok sorrendje 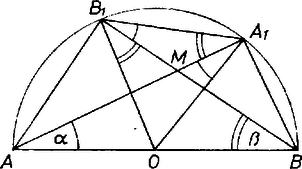$A$ , $B_{1}$ , $A_{1}$ , $B$ .

Jelöljük az

O A A_{1}

O B B_{1}

szögeket

α

-val,

β

-val, akkor az egyenlő szárú

O A A_{1}

O B B_{1}

háromszögekben az

O A_{1} A

O B_{1} B

is rendre

α

-val,

β

-val egyenlő, továbbá a kerületi szögekre vonatkozó tétel miatt

B B_{1} A_{1} ∢ = α

A A_{1} B_{1} ∢ = β

. Tehát az egyenlő szárú

A_{1} B_{1} O

háromszögben az

A_{1} B_{1}

alapon levő szögek

(α + β)

-val egyenlőek. Ezek a szögek így egyenlőek az

A B M

háromszög

M

-beli külső szögével,

(180^{\circ} - A M B ∢)

-gel. Ez a feladatban szereplő

\begin{matrix} A M B ∢ + A_{1} O B_{1} ∢ = 180^{\circ} \end{matrix}

feltétel miatt ekvivalens azzal, hogy az

A_{1} B_{1} O

háromszög szögei egyenlőek, vagyis ez a háromszög szabályos. Ez pedig azt jelenti, hogy az

A_{1} O B_{1} ∢ 60^{\circ}

-os, az

A M B ∢

pedig

120^{\circ}

-os.
A kérdezett mértani hely tehát azon

M

pontok összessége, amelyekből az

A B

szakasz

120^{\circ}

alatt látszik. Mint tudjuk, ez két körívből áll, amelyek az

A B

fölé rajzolható két szabályos háromszög köré írt körének az eredeti körbe eső ívei.