Kezdőlap


Feladat:	Gy.1707	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1978/január, 19 - 20. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1977/szeptember: Gy.1707

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a $C$ pontnak az $x$ tengelyre való vetületét $E$ -vel. Az $A B C D$ négyszög területe helyett a vele egyenlő területű $A E C D$ négyszög területét fogjuk kiszámítani. Először azonban lássuk be, hogy e két terület valóban egyenlő.
Húzzunk a $B$ ponton át párhuzamost az $A C$ átlóirányú egyenessel, ez szintén átló irányú lesz, azaz átmegy a $B$ csúccsal átellenes $E$ -n. Az $A B C$ és $A E C$ háromszögek közös alapja $A C$ , az ehhez tartozó magasságok is egyenlők, hiszen párhuzamos egyenesek közé esnek, ezért a két háromszög területe egyenlő, $\frac{49}{2}$ területegység. Ezzel igazoltuk a két négyszög területének egyenlőségét.
Az $A C$ szakasz hosszát Pitagorasz tétellel számítjuk ki:

\begin{matrix} \bar{A C} = \sqrt[]{7^{2} + 7^{2}} = \sqrt[]{98} . \end{matrix}

Mivel

A C < 10

, az

A

és

C

pontokból húzott

5

egység sugarú körívek valóban metszik egymást a

D_{1}

és

D_{2}

pontokban, melyek az

A C

egyenesre tükrösek.
Konkáv négyszög abban az esetben jön létre, ha a metszéspont az

A C

egyenesnek az

x

tengely felőli oldalára esik. Ekkor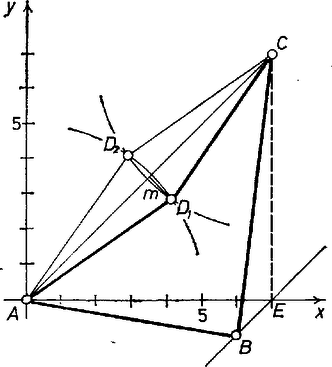

T_{A B C D_{1}} = T_{A E C} - T_{A D_{1} C}

Ki kell még számítanunk az

A D_{1} C

háromszög területét, amelyben

\bar{A C} = \sqrt[]{98}

\bar{A D_{1}} = \bar{D_{1} C} = 5

. Az

A C

oldalhoz tartozó

m

magasság hosszát Pitagorasz tétellel számítjuk ki.

\begin{matrix} m = \sqrt[]{5^{2} - {(\frac{\sqrt[]{98}}{2})}^{2}} = \sqrt[]{\frac{1}{2}}, \\ t = \frac{A C \cdot m}{2} = \frac{\sqrt[]{98} \cdot \sqrt[]{\frac{1}{2}}}{2} = \frac{7}{2} . \end{matrix}

Így a négyszög területe

\begin{matrix} \frac{49}{2} - \frac{7}{2} = 21 \end{matrix}

területegység.
A szimmetria miatt az

A D_{2} C

háromszög területe egyenlő az

A D_{1} C

háromszög területével, s igy konvex esetben az

A D_{1} C B

négyszög területe éppen az

A D_{1} C

háromszög területével lesz nagyobb, mint az

A E C

háromszög területe.

A D_{2} C B ter. = \frac{49}{2} + \frac{7}{2} = 28

területegység.