| Feladat: | Gy.1701 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1978/március, 107 - 108. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Középvonal, Kombinatorikus geometria térben, Konstruktív megoldási módszer, Tetraéderek, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1977/május: Gy.1701 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A tetraéder hat éle közül kétféleképpen választhatunk ki négyet: vagy úgy, hogy közülük három egy síkban van, vagy úgy, hogy nincs közöttük három egy síkban. Az első esetben a felezőpontok nincsenek egy síkban, a másodikban viszont nemcsak egy síkban vannak, de paralelogrammát is alkotnak. Ennek megfelelően két esetet különböztetünk meg. 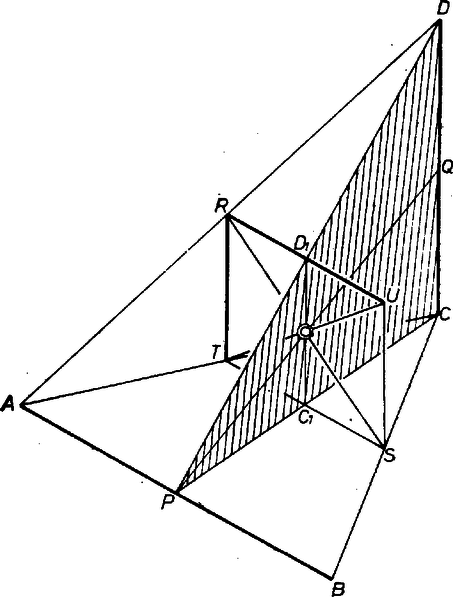 a) Az adott pontok nincsenek egy síkban. Válasszunk ki közülük tetszés szerint hármat, és húzzunk az általuk meghatározott háromszögben a csúcsokon át a szemközti oldalakkal párhuzamosakat. Így megkapjuk azt a három élt, amelyik egy síkban van. Az általuk alkotott lap tetszőleges csúcsait összekötve a negyedik adott ponttal, és a kapott egyenesre a csúcstól a pontig terjedő szakaszt mégegyszer felmérve a tetraéder negyedik csúcsát kapjuk. Eljárásunk helyessége és az, hogy így az összes megfelelő tetraédert megkapjuk, nyilvánvaló. Összesen tetraédert kapunk, mert először , másodszor eset között választhatunk. b) Az adott pontok egy síkban vannak. Ebben az esetben csak akkor van megoldás, ha a pontok paralelogrammát alkotnak. Ennek átlóihoz egy tetszőleges, velük nem egy síkban levő szakaszt felvéve, melynek felezőpontja azonos az átlók felezőpontjával, megkapjuk a hiányzó két élfelezőpontot. Most tehát adott három szakasz, , , , amelyek nincsenek egy síkban, de a felezőpontjuk azonos. Húzzunk párhuzamost -n át mondjuk -val, és mérjük fel rá -ből kiindulva mindkét irányba az szakaszt, -n át pedig -vel húzzunk párhuzamost, és erre -ből kiindulva az szakaszt mérjük fel mindkét irányba. Jelöljük a kapott végpontokat rendre , , , -vel, felezőpontját -gyel, felezőpontját -gyel. Mivel is felezi -t, mint és , továbbá párhuzamos -vel, és fele annak, a háromszög középvonala. Így mondjuk a , a szakaszt felezi. Emiatt viszont az , pedig az háromszög középvonala, hiszen felezik -t, illetve -t, párhuzamosak -vel, és féle akkorák, mint . Tehát az tetraéderben , , , , , valóban élfelezőpontok. Ebben az esetben tehát végtelen sok megoldás van. |