Kezdőlap


Feladat:	Gy.1695	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Molnár Gábor
Füzet:	1977/november, 145 - 146. oldal		PDF \| MathML
Témakör(ök):	Térgeometria alapjai, Szögfüggvények a térben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1977/április: Gy.1695

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $a$ , $b$ , $c$ egyenesek közös pontját $O$ -val és legyen $C$ a $c$ egyenesnek az a pontja, amelyre 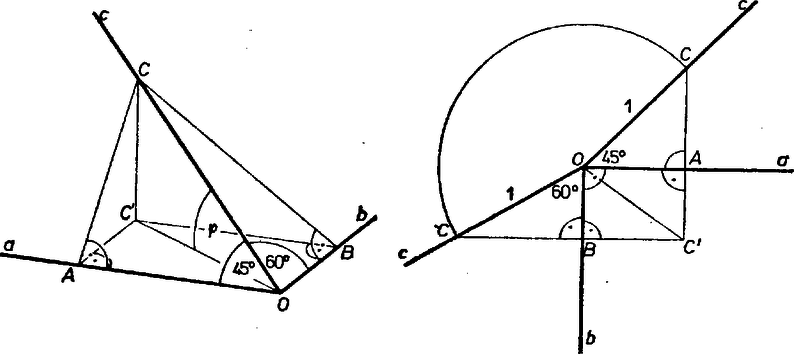$O C = 1$ .
Mivel $c$ nem merőleges az $S = [a, b]$ síkra, a síkkal bezárt szögét a síkra merőleges vetületével bezárt szöge adja. Jelöljük $C$ vetületét $S$ -re $C'$ -vel. Meg akarjuk határozni a $C O C' ∢ = φ$ szöget. Bocsássunk $C'$ -ből merőlegest az $a$ , ill. $b$ egyenesre és jelöljük a merőlegesek talppontját $A$ -val, ill. $B$ -vel.

Mivel

C' A ⊥ a

és

b ⊥ a

, következik, hogy

C' A

egyenes párhuzamos

b

-vel. Hasonlóban

C' B ⊥ b

és

a ⊥ b

-ből

C' B ‖ a

. Így

O A C' B

négyszög téglalap és

O A = C' B

O B = C' A

. Az

O A

, ill.

O B

szakaszok hosszának meghatározásához lássuk be, hogy

O A C

és

O B C

háromszög derékszögű. Ismeretes, hogy ha egy egyenes merőleges egy sík két (nem párhuzamos) egyenesére, akkor a sík minden egyenesére merőleges. A

C C' ⊥ S

így

C C' ⊥ a

, de

C' A ⊥ a

. Az

a

egyenes tehát a

C C' A

sík két egyenesére merőleges, de akkor minden egyeneséremerőleges, így

A C

-re is. Hasonlóan igazolhatjuk, hogy

O B ⊥ C B

.
Mivel

C O A ∢ = 45^{\circ}

C O B ∢ = 60^{\circ}

és

\bar{O C} = 1

\bar{O A} = \frac{\sqrt[]{2}}{2}

\bar{O B} = \frac{1}{2}

.
Így az

O A C' B

téglalap átlója

O C' = \sqrt[]{{(\frac{\sqrt[]{2}}{2})}^{2} + {(\frac{1}{2})}^{2}} = \frac{\sqrt[]{3}}{2}

és az

O C C'

derékszögű háromszögből

\begin{matrix} cos φ = \frac{\sqrt[]{3}}{2} azaz φ = 30^{\circ} . \end{matrix}

Molnár Gábor (Zalaegerszeg, Zrínyi M. Gimn., I. o. t.)