Feladat:	Gy.1694	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1977/december, 207 - 208. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek nevezetes tételei, Körülírt kör, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1977/április: Gy.1694

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle \text{sin}\alpha +\text{sin}\beta +\text{sin}\gamma >2.}\end{array}$ (1) Tegyük fel, hogy az $ABC$ háromszögben $AC\ge BC$, és jelöljük a háromszög köré írható kört $k$-val, sugarát $r$-rel. Ismeretes, hogy ${\displaystyle \begin{array}{c}\hfill {\displaystyle \overline{AB}=2r\text{sin}\gamma \mathrm{,}\overline{BC}=2r\text{sin}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle \overline{CA}=2r\text{sin}\beta }\hfill \end{array}}$ így (1) ekvivalens azzal, hogy $\begin{array}{c}{\displaystyle \overline{AB}+\overline{BC}+\overline{CA}>4r\mathrm{.}}\end{array}$ (2) Jelöljük $k$-nak $A$-val átellenes pontját $C_0$-lal, és az $AB{C}_0$ háromszög $C_0$-beli külső szögfelezőjének $k$-val alkotott második metszéspontját 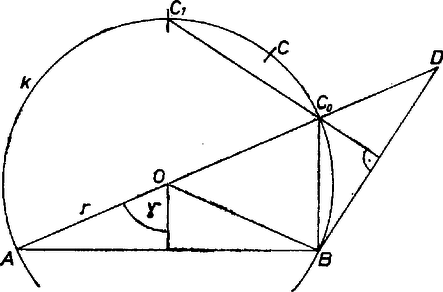$C_1$-gyel.     $C_1$ felezi a nagyobbik $AB$ ívet, és feltevéseink szerint $C$ a $C_0{C}_1$ íven van. Mivel a $C_0{C}_1$ egyenes külső szögfelező, $B$-t $C_0{C}_1$-re tükrözve az $A{C}_0$ egyenes $C_0$-on túli meghosszabbításán levő pontot kapunk, jelöljük ezt $D$-vel. Az egész $C_0{C}_1$ ív a $BD$ szakasz $C_0{C}_1$ felező merőleges egyenesének $D$-t tartalmazó oldalán van, ezért $\overline{BC}\ge \overline{DC}$. Az $ACD$ háromszögben $\overline{AC}+\overline{CD}>\overline{AD}$, az $AB{C}_0$ háromszögben pedig $\overline{AB}+\overline{B{C}_0}\ge \overline{A{C}_0}$. Ezek alapján $\begin{array}{c}{\displaystyle \overline{AB}+\overline{BC}+\overline{CA}\ge \overline{AB}+\overline{DC}+\overline{CA}>\overline{AB}+\overline{AD}=\overline{AB}+\overline{B{C}_0}+\overline{A{C}_0}>2\overline{A{C}_0}=4r\mathrm{,}}\end{array}$ amint azt bizonyítani akartuk.   Megjegyzés. Belátható, hogy a $0<x<\pi$ szakaszon $\frac{\text{sin}x}{x}$ az $x$ monoton fogyó függvénye. Emiatt esetünkben a $\frac{\text{sin}\alpha }{\alpha }$ , $\frac{\text{sin}\beta }{\beta }$ , $\frac{\text{sin}\gamma }{\gamma }$ hányadosok mindegyike nagyobb $\frac{\text{sin}\pi /2}{\pi /2}=\frac{2}{\pi }$-nél és így $\text{sin}\alpha +\text{sin}\beta +\text{sin}\gamma >\left(\alpha +\beta +\gamma \right)\frac{2}{\pi }=2$.