Feladat: Gy.1689 Korcsoport: 16-17 Nehézségi fok: -
Megoldó(k):  Banyár J. ,  Becze I. ,  Bene Gy. ,  Benkő T. ,  Blázsik Z. ,  Buczolich Z. ,  Bölcsföldi L. ,  Csányi Noémi ,  Csikós B. ,  Csordás A. ,  Filakovszky P. ,  Gát Gy. ,  Gyuris Zs. ,  Hajnal P. ,  Héder J. ,  Horváth Á. ,  Horváth M. ,  Horváth T. ,  Kántor S. ,  Kántor Zs. ,  Kátai I. ,  Kiss 352 Gy. ,  Kóta Erika ,  Kozma L. ,  Lakatos I. ,  Lukács 258 Erzsébet ,  Molnár 267 T. ,  Nagy 221 A. ,  Németh 892 R. ,  Németh Ágnes ,  Oláh K. ,  Pacher T. ,  Pintér L. ,  Pósafalvi A. ,  Spilkó J. ,  Szabó 200 Ágnes ,  Szalkai I. ,  Szemes Gy. ,  Szendrei G. ,  Varga L. ,  Varga T. ,  Verőházi Mária ,  Winkler R. 
Füzet: 1978/május, 205 - 206. oldal  PDF  |  MathML 
Témakör(ök): Térfogat, Térgeometriai bizonyítások, Tetraéderek, Gyakorlat
Hivatkozás(ok):Feladatok: 1977/március: Gy.1689

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha az A, B, C pontok egy egyenesen vannak, (1) miatt B' is, C' is benne van az e és AA' által meghatározott síkban, és emiatt rajta vannak ennek a síknak P'-vel alkotott metszésvonalán is. Így tehát az A, B, C és az A', B', C' pontok egyszerre eshetnek csak egy egyenesre, amikor a mondott térfogatok 0-val egyenlőek.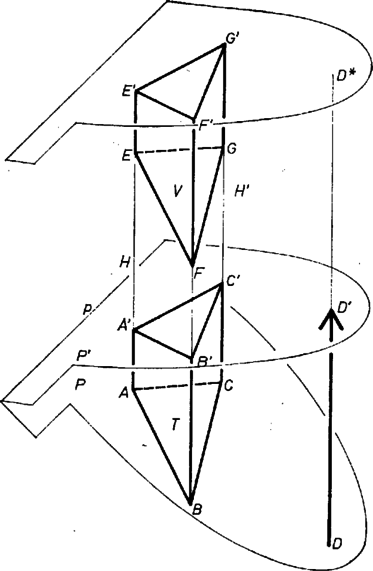

 
 

A továbbiakban feltesszük, hogy az AA', BB', CC' egyenesek nincsenek egy síkban. Toljuk el a T=ABCA'B'C' testet a DD→' vektorral és jelöljük az új testet V-vel, csúcsait rendre E, F, G, E', F', G'-vel. (1) miatt V csúcsai rendre rajta vannak az AA', BB', CC' egyeneseken, így a H=ABCEFG és H'=A'B'C'E'F'G' hasábok alkotó egyenesei azonosak. Ha H-hoz hozzávesszük V-t, akkor ugyanazt a testet kapjuk, mintha H'-hoz hozzávennénk T-t, vagyis
H+V=H'+T.(2)

Mivel itt T és V egybevágóak, ebből következik, hogy H és H' térfogata egyenlő.
Tudjuk, hogy az eltolás a síkot síkba viszi át, D' rajta van az EFG síkon, és H magassága egyenlő az ABCD' tetraéder D'-höz tartozó magasságával. Ennek a két testnek ABC lapja közös, tehát H térfogata háromszorosa ABCD' térfogatának. Toljuk el D'-t is a DD' vektorral, a kapott pont legyen D*. Ez egyrészt benne van az E'F'G' síkban, másrészt ugyanolyan messze van P'-től, mint D. A H' hasáb magassága tehát egyenlő az A'B'C'D tetraéder D-hez tartozó magasságával, és H' térfogata háromszorosa A'B'C'D térfogatának. Láttuk már, hogy H és H' térfogata egyenlő, ezzel a bizonyítást befejeztük.
 

Megjegyzések. 1. Nem használtuk ki, hogy V és T diszjunktak, ami általában nem is igaz. Az efféle átdarabolásoknál mindig célszerűbb előbb hozzávenni az egyik testhez valamit (esetünkben T-hez H'-t), és csak aztán elvenni egy másik darabot az egyesítés révén kapott testből (T+H'-ből V-t). Tulajdonképpen arra is csak a szemléletesség kedvéért volt szükségünk, hogy T test. Ezt a feladatnak az a feltétele biztosította, hogy a vizsgált pontok egy-egy félsíkban vannak benne. Igaz marad azonban a feladat állítása akkor is, ha benne a félsíkokat síkokkal helyettesítjük.
2. Belátható a feladat állítása annak alapján is, hogy a párhuzamos vetítés nem változtatja meg a területarányokat.