Kezdőlap


Feladat:	Gy.1666	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Varga Dániel
Füzet:	1977/szeptember, 20. oldal		PDF \| MathML
Témakör(ök):	Hossz, kerület, Körök, Gyakorlat
Hivatkozás(ok):	Feladatok: 1976/december: Gy.1666

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük az $A B$ , $B C$ , $C D$ , $D E$ , $E F$ , $F A$ ívekhez tartozó kerületi szögeket (1. ábra), ezek rendre:

\begin{matrix} A E B ∢, B E C ∢, C A D ∢, D A E ∢, E C F ∢, F C A ∢ . \end{matrix}

1. ábra

Összegük éppen az

A C E

háromszög belső szögeinek összege, azaz

π

. Az említett ívek különböző körökön fekszenek, de mivel a körök sugarai egyenlők, egyetlen kör ívének is tekinthetjük őket. A

H

kerületéhez tartozó középponti szög tehát

2 π

, és mivel a kör sugara egységnyi, ez éppen azt jelenti, hogy

H

területe

2 π

.
Az állítás akkor is igaz, ha a három kör egy ponton megy át, s hasonlóképpen bizonyítható. A megfelelő ívekhez tartozó kerületi szögek összege most az

A B C

háromszög belső szögeinek összegét adja (2. ábra), azaz ugyancsak

π

. Amiből ugyanúgy következik a feladat állítása, mint az első esetben.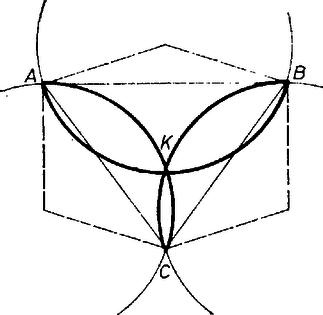

2. ábra

Varga Dániel (Budapest, Berzsenyi D. Gimn., II. o. t.)