Feladat: Gy.1664 Korcsoport: 16-17 Nehézségi fok: könnyű
Füzet: 1977/április, 161 - 162. oldal  PDF  |  MathML 
Témakör(ök): Körülírt kör, Beírt kör középpontja, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1976/december: Gy.1664

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen ABC tetszőleges háromszög, melynek k a körülírt köre és P a beírt kör középpontja. Jelöljük a CP egyenes k-val alkotott második metszéspontját C1-gy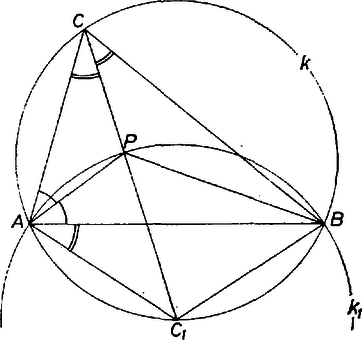el.

 

 

Ismeretes, hogy C1 felezi az őt tartalmazó AB ívet, és így AC1=BC1. Az ACP háromszögnek APC1 külső szöge, tehát
APC1∢=PAC∢+PCA∢.(1)
Mivel PA, PC felezi az ABC háromszög A-nál, C-nél levő szögeit, PAC∢=PAB∢, PCA∢=PCB∢. Ez utóbbi viszont a kerületi szögek tétele miatt egyenlő a BAC1 szöggel. Ezek szerint
PAC∢=PAB∢,PCA∢=BAC1∢,(2)
és így APC1∢=PAC1∢, vagyis az APC1 háromszögben AC1=PC1. Tehát a C1 középpontú, A-n, B-n átmenő k1 kör átmegy P-n.
Ezek alapján a szerkesztés menete a következő. Legyen C a k kör tetszőleges pontja, C1 a CP egyenes k-val alkotott második metszéspontja, és A, B a C1 középpontú, P-n átmenő k1 kör k-val alkotott metszéspontjai. Amiatt, hogy P a k belső pontja, a mondott metszéspontok valóban léteznek. Mivel AC1=BC1, PC az ABC háromszög belső szögfelezője. P az AB-nek ugyanazon az oldalán van, mint C, hiszen ott van k1-nek P-n átmenő AB íve is. Így P az ABC háromszög belső pontja. Elég megmutatnunk, hogy PA felezi a háromszög A-nál levő szögét, hiszen így már két szögfelezőről fogjuk tudni, hogy átmegy P-n, tehát beláttuk, hogy az ABC háromszögnek megvannak a kívánt tulajdonságai. Mivel most tudjuk, hogy APC1 egyenlőszárú, és továbbra is fennáll (1), elég a (2) alatti egyenlőségek közül az egyiket belátni, abból már következik a másik. A kerületi szögek tétele miatt BAC1∢=BCC1∢ és azt már tudjuk, hogy CC1 szögfelező, tehát BCC1∢=C1CA∢, ami viszont azonos a PCA szöggel. A megszerkesztett háromszög tehát valóban megfelelő.
 

Megjegyzés. Többet láttunk be, mint kellett, hiszen a C csúcsot is tetszőlegesen vettük fel. Ha PC átmérő k-ban, ABC egyenlőszárú lesz, és általában C megválasztásával meghatározhatjuk az ABC háromszög alakját. Meglepő tétele Eulernek, hogy viszont az ABC-be írt kör sugara nem függ C megválasztásától. Javasoljuk az olvasónak, próbálja meg belátni ezt a nevezetes állítást. Mi például a 43. kötetünk 198‐199. oldalain közöltünk rá két bizonyítást, közülük a második azonos a Kürschák‐Hajós‐Neukomm‐Surányi: Matematikai versenytételek I. 3. kiadás 40. oldalán találhatóval.