Kezdőlap


Feladat:	Gy.1654	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1977/február, 73 - 74. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Középpontos tükrözés, Hossz, kerület, Terület, felszín, Négyszögek geometriája, Szélsőérték-feladatok differenciálszámítás nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1976/október: Gy.1654

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsünk egy tetszőleges $A B C D$ négyszöget, és húzzuk meg az egyik átlóját, legyen ez az 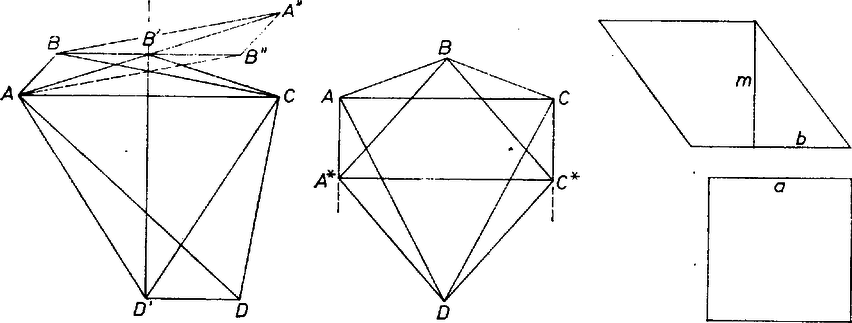$A C$ .
Ismeretes, hogy ha a $B$ és $D$ csúcsokat ezen átlóval párhuzamos egyenes mentén eltoljuk, a négyszög területe nem változik. Legyen $B$ , $D$ új helyzete $B'$ , $D'$ .

Először azt látjuk be, hogy az

A B' C D'

négyszög kerülete akkor a legkisebb, ha

B'

D'

A C

átló felező merőlegesén van, azaz a négyszög deltoid.
Tükrözzük az

A

és

B

pontokat a

B'

pontra, képük rendre

A''

és

B''

, ekkor

\begin{matrix} A B + B C = A B + B A'' > 2 A B' = A B' + B' C . \end{matrix}

Másodszor belátjuk, hogy az egyenlő területű deltoidok közül a rombusz kerülete a legkisebb. A bizonyítást az előzőhöz hasonlóan végezhetjük, arra a két csúcsra, amely nem a szimmetriatengelyen fekszik. Ezeket eltolva, úgy hogy a felezőmerőlegesre kerüljenek, a kerület ismét csökkenni fog.
Végül tekintsünk két egyenlő területű rombuszt és négyzetet. A négyzet oldala legyen

a

, a rombusz oldala

b

, magassága

m

. Ekkor

t = b m = a^{2}

.
Kerületük

4 a

, ill.

4 b

. Mivel

b \geq m

b^{2} \geq a^{2}

, és

a

és

b

pozitív, így

4 b \geq 4 a

, egyenlőség csak akkor állhat fenn, ha

b = m

.
Válaszunk tehát: az egyenlő területű négyszögek közül a négyzet kerülete a legkisebb.