Kezdőlap


Feladat:	Gy.1647	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1977/január, 18 - 19. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Koszinusztétel alkalmazása, Alakzatok köré írt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1976/szeptember: Gy.1647

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük, a $\sqrt[]{2}$ nagyságú oldalakhoz tartozó középponti szöget $α$ -val, a $\sqrt[]{24}$ -hez tartozót $β$ -val. Mivel a sokszög konvex, a kerületén körbejárva egy irányban egyszer kerüljük meg a kör középpontját, így

\begin{matrix} 6 α + 6 β = 360^{\circ}, α + β = 60^{\circ} . \end{matrix}

Biztosan van a sokszögnek olyan csúcsa, amelyben egy

\sqrt[]{2}

és egy

\sqrt[]{24}

nagyságú oldal csatlakozik egymáshoz, jelöljük ezek egyikét

B

-vel, a szomszédos csúcsok közül

A

legyen a

\sqrt[]{2}

C

\sqrt[]{24}

nagyságú oldal másik végpontja. A kör középpontját jelöljük

O

-val. Az

A B C O

négyszög

A

-nál,

B

-nél,

C

-nél levő szögének összege

360^{\circ} - 60^{\circ} = 300^{\circ}

, és mivel az

A B O

B C O

háromszögek egyenlő szárúak,

\begin{matrix} O A B ∢ = A B O ∢, O B C ∢ = B C O ∢, \end{matrix}

tehát a négyszög

B

-nél levő szöge egyenlő az

A

-nál,

C

-nél levő szögek összegével:

\begin{matrix} A B C ∢ = 150^{\circ} . \end{matrix}

(1)

Legyen általában egy

A B C

háromszögben

A B = c

B C = a

, és

A B C ∢ = 150^{\circ}

. Jelöljük

A

-nak a

B C

egyenesen levő vetületét

D

-vel, és

A

-nak

D

-re vonatkozó tükörképét

E

-vel. Az

A B D

háromszög derékszögű, és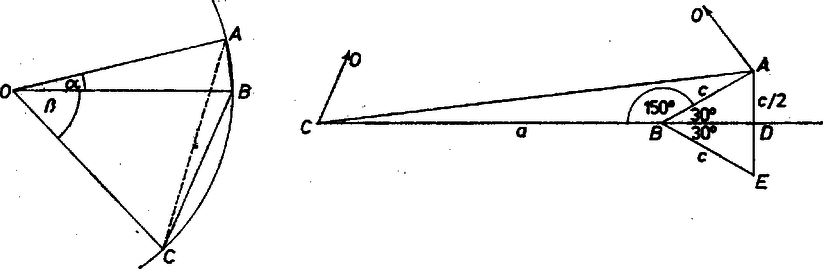

\begin{matrix} A B D ∢ = 180^{\circ} - 150^{\circ} = 30^{\circ} . \end{matrix}

Emiatt

A B E

szabályos háromszög, és

\begin{matrix} A D = c / 2, B D = c \frac{\sqrt[]{3}}{2} . \end{matrix}

A C D

derékszögű háromszögben Pitagorasz tétele szerint

\begin{matrix} A C^{2} = {(a + c \frac{\sqrt[]{3}}{2})}^{2} + {(\frac{c}{2})}^{2} = a^{2} + c^{2} + a c \sqrt[]{3} . \end{matrix}

(2)

Esetünkben

a = \sqrt[]{24}

c = \sqrt[]{2}

, tehát

A C^{2} = 24 + 2 + \sqrt[]{24 \cdot 2 \cdot 3} = 38

A C = \sqrt[]{38} = 6, 164

Megjegyzés. Megkaphattuk volna (2)-t (1)-ből a cosinus-tétel segítségével is. Megoldásunkban tulajdonképpen elmondtuk a tétel bizonyítását az

A B C ∢ = 150^{\circ}

eset adta egyszerűsítésekkel élve.