Feladat: Gy.1646 Korcsoport: 14-15 Nehézségi fok: átlagos
Füzet: 1977/január, 17 - 18. oldal  PDF  |  MathML 
Témakör(ök): Körülírt kör, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):Feladatok: 1976/szeptember: Gy.1646

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A B és C pont az A körül fordulhat el, ezért ha egy P pont a keresett mértani hely egy pontja, akkor az A körüli AP sugarú kör minden pontja is pontja a mértani helynek.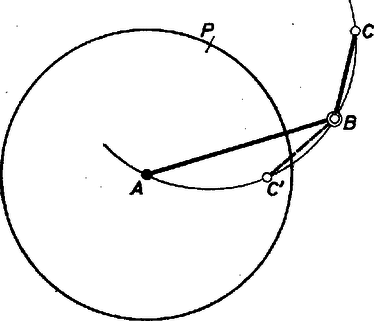

 

 

Vizsgáljuk meg, hogy mi a szükséges feltétele annak, hogy egy P pont a mértani helyhez tartozzon. Nyilván az, hogy a P pont körüli AP sugarú körben lehessen az adott AB és BC szakaszokkal háromszöget szerkeszteni. Vagyis AB és BC az AP sugarú körnek húrja, és így
AB≤2APésBC≤2AP
kell, hogy legyen.
Adott AB és BC szakasz esetén, tehát a mértani helyhez tartozik a sík minden olyan pontja, amelynek A-tól való távolsága nagyobb vagy egyenlő az AB/2, BC/2 szakaszok közül a nagyobbiknál.
A sík tetszőleges P pontjához tudunk háromszöget szerkeszteni, ha AP≥max(AB/2,BC/2) a következőképpen; rajzoljunk P körül egy AP sugarú kört, ez lesz a keresett háromszög körülírt köre (P a középpont), mérjük fel a kör kerületére A-ból kiindulva az AB és BC szakaszokat. A háromszög mindig létrejön, kivéve, ha AB=BC=2AP, ekkor ugyanis A≡C, így nem jön létre háromszög.