Kezdőlap


Feladat:	Gy.1635	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1977/szeptember, 16 - 17. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Térgeometriai bizonyítások, Térgeometriai számítások trigonometria nélkül, Tetraéderek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1976/április: Gy.1635

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C$ háromszög síkját $Σ$ -val, a feladat szerint $S D ⊥ Σ$ . Emiatt $A D S$ derékszögű, és $A$ -nál levő szöge azonos $S A$ -nak $Σ$ -val bezárt szögével. Az $A D S$ háromszög tehát egyenlő szárú is, benne $A S = 2 a$ miatt $A D = D S = a \sqrt[]{2}$ . Tudjuk, hogy a $B, C$ pontok rajta vannak a $Σ$ -bel $A$ körüli, $a$ sugarú $k$ körön is, és az $S$ körüli, $a \sqrt[]{3}$ sugarú $g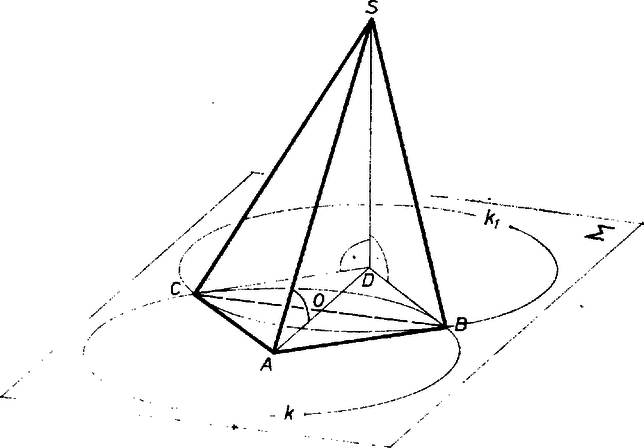$ gömbön is.

Mivel

S D = a \sqrt[]{2} < a \sqrt[]{3}, g

metszi

Σ

-t, mégpedig egy

D

körüli,

\sqrt[]{{(a \sqrt[]{3})}^{2} - {(a \sqrt[]{2})}^{2}} = a

sugarú

k_{1}

körben. Annak az

A B^{*} D C^{*}

négyzetnek, amelynek

A D

az egyik átlója, a

B^{*}

C^{*}

csúcsai rajta vannak

k

-n is,

k_{1}

-en is, mivel pedig két különböző körnek legfeljebb két közös pontja lehet, a

B

C

pontok (valamilyen sorrendben) azonosak a

B^{*}

C^{*}

csúcsokkal, tehát az

A B D C

négyszög négyzet.
Jelöljük az

A B D C

négyszög centrumát

O

-val, akkor

O S^{2} = O D^{2} + D S^{2} = (\frac{1}{2} + 2) a^{2} = \frac{5}{2} a^{2},

tehát

B C S

területe

\frac{1}{2} \sqrt[]{2} \sqrt[]{\frac{5}{2}} a^{2}

. Az

A B S

A C S

háromszögek egybevágóak,

A B = a

B S = a \sqrt[]{3},

A S = 2 a

miatt együtt egy

2 a

oldalú szabályos háromszöget tesznek ki. Területük

\frac{1}{2} \frac{\sqrt[]{3}}{4} {(2 a)}^{2}

. Végül

A B C

területe

\frac{1}{2} a^{2}

, tehát a tetraéder felszíne

\begin{matrix} F = \frac{a^{2}}{2} (1 + \sqrt[]{3} + \sqrt[]{5}) . \end{matrix}