Kezdőlap


Feladat:	Gy.1630	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1976/december, 206 - 207. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Háromszögek egybevágósága, Gyakorlat
Hivatkozás(ok):	Feladatok: 1976/március: Gy.1630

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A_{1} B_{1} C_{1}$ , $A_{2} B_{2} C_{2}$ legyen olyan két egybevágó háromszög, amelyik párhuzamos eltolással egymásba vihető. Jelöljük az eltolás vektorát, azaz azt a vektort, amely $A_{1}$ -et $A_{2}$ -be, $B_{1}$ -et $B_{2}$ -be, $C_{1}$ -et $C_{2}$ -be viszi át, v-vel. Az $A_{1} A_{13} = \frac{1}{2} A_{1} A_{3}$ , $A_{2} A_{23} = \frac{1}{2} A_{2} A_{3}$ , így $A_{13} A_{23} = \frac{1}{2} v$ , és ugyanez teljesül a $B_{13} B_{23}$ , $C_{13} C_{23}$ vektorokra is. Vagyis a két háromszög csúcsai ugyanakkora nagyságú és irányú eltolással vihetők át egymásba.^{$^{*}$}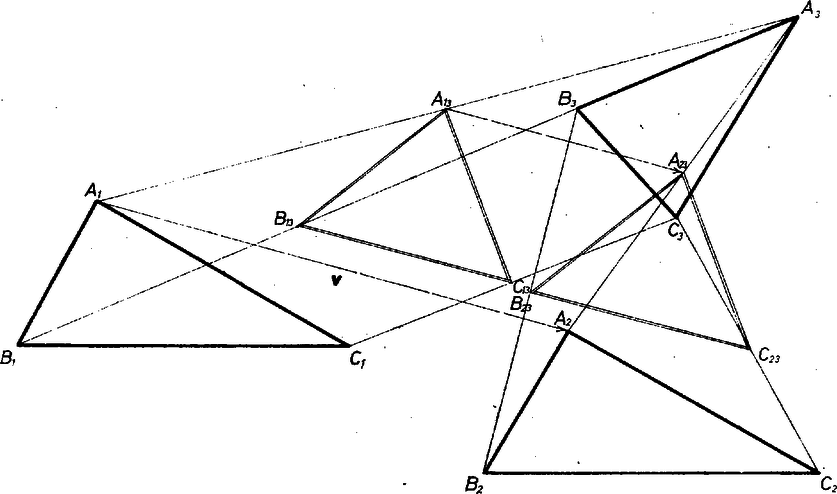

Ha az

A_{1} B_{1} C_{1}

háromszög és

A_{2} B_{2} C_{2}

háromszög egybevágó és megfelelő oldalai párhuzamosak, de nem vihetők át egymásba párhuzamos eltolással, akkor a két háromszög pontra nézve szimmetrikus. Szimmetriaközéppontjuk

A_{1} = A_{2}

, és

| \vec{C_{1} B_{1}} | = | \vec{C_{2} B_{2}} |

egyező nagyságú, de ellentétes irányú vektorok. Kössük össze a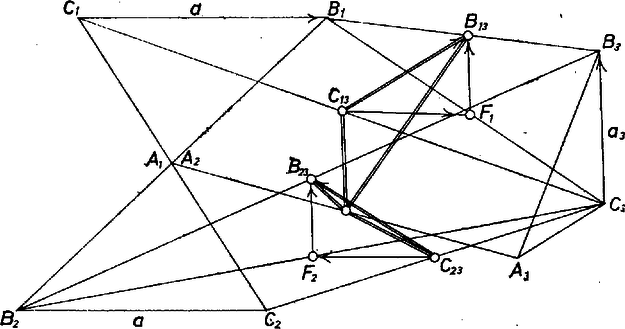

C_{3}

pontot

B_{1}

-gyel és

B_{2}

-vel.

C_{3} B_{1}

felezőpontja

F_{1}

C_{3} B_{2}

felezőpontja

F_{2}

\vec{C_{3} B_{3}} = a_{3}

;

\vec{C_{13} F_{1}} = \frac{1}{2} a

\vec{F_{1} B_{3}} = \frac{1}{2} a_{3}

;

\vec{C_{23} F_{2}} = - \frac{1}{2} a

;

\vec{F_{2} B_{23}} = \frac{1}{2} a_{3}

, ekkor

\begin{matrix} \vec{C_{13} B_{23}} = \frac{1}{2} (a + a_{3}), \vec{C_{23} B_{23}} = \frac{1}{2} (-a + a_{3}), \end{matrix}

és e két eredmény általában nem egyezik. Így ebben az esetben az állítás általában nem igaz.

^{$^{*}$}A kitűzéskor a feladatok számozásába hiba csúszott, az 1630-as gyakorlat kétszer jelent meg. A

g

jelzés a feladat geometriai jellegére utal.