Feladat:	Gy.1627	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1981/november, 135 - 138. oldal		PDF  |  MathML
Témakör(ök):	Játékelmélet, játékok, Sakktáblával kapcsolatos feladatok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1976/március: Gy.1627

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. I. Azt mondjuk, hogy a figurák valamely sorban vagy oszlopban "jól helyezkednek el'', ha a sor vagy oszlop középső mezője üres, és az üres mező egyik oldalán csupa fekete, másik oldalán csupa fehér figura áll. A kiindulási ábrán a középső oszlopban és a középső sorban helyezkednek el jól a figurák. Be fogjuk látni, hogy ha valamely oszlopban vagy sorban a figurák jól helyezkednek el, akkor ebben az oszlopban, ill. sorban a fekete és a fehér figurák $n\left(n+2\right)$ lépésben felcserélhetők a többi oszlopban, ill. sorban álló figura mozgatása nélkül. Fogadjuk el egyelőre ezt az állítást bizonyítás nélkül. Ebből következik, hogy a kiindulási ábrán a középső oszlop fekete és fehér figurái a többi oszlop figuráinak mozgatása nélkül $n\left(n+2\right)$ lépésben felcserélhetők. Hajtsuk végre ezt a cserét. Nyilvánvaló, hogy a csere során a középső oszlop minden mezője legalább egyszer üresen marad: a középső mező rögtön kezdetben üres, a többi mezőre pedig ellentétes színű figurának kell kerülnie ‐ ehhez pedig előbb ki kell üríteni a mezőt. Vegyük észre, hogy amikor a $k$-adik mezőt először ürítjük ki, a tábla $k$-adik sorában a figurák jól fognak elhelyezkedni! Következésképp a $k$-adik sor figurái most $n\left(n+2\right)$ lépésben felcserélhetők, a többi sor figuráinak elmozdítása nélkül (vagyis a középső oszlop többi mezőjén a figurák helyzete eközben nem változik). Ha a $k$-adik sorban a cserét végrehajtjuk, akkor a csere végén a $k$-adik sor középső mezője megint üres lesz, tehát a középső oszlopban a figurák megint úgy fognak elhelyezkedni, mint a csere előtt. A középső oszlopban tehát ott folytathatjuk eljárásunkat, ahol abbahagytuk. Ha a középső oszlopban úgy hajtjuk végre a cserét, hogy amikor valamelyik mező először válik üressé, akkor az eljárást megszakítjuk, és a megfelelő sor cseréjét közbeiktatjuk, akkor eljárásunk végére az $1.$, $2.$, $\text{...}$, $n\mathrm{.}$ oszlop fekete figuráit felcseréljük az $n+2.$, $n+3.$, $\text{...}$, $2n+1$. oszlop fehér figuráival és a középső oszlopban felcseréljük egymással a fekete és a fehér figurákat. Tehát a teljes cserét végrehajtottuk. Nézzük, hány lépésből áll az eljárásunk! A középső oszlopban a cseréhez $n\left(n+2\right)$ lépés kell. A sorokon belüli cserét mindig akkor kezdjük végrehajtani, amikor épp ebben a sorban helyezkednek el jól a figurák, így egy sor cseréjéhez is elég $n\left(n+2\right)$ lépés. Összesen $2n+1$ sorban és egy oszlopban kell tehát egyenként $n\left(n+2\right)$ lépést tennünk, vagyis eljárásunk összesen $\left(2n+2\right)n\left(n+2\right)=2n\left(n+1\right)\left(n+2\right)$ lépésből áll. Ezzel bebizonyítottuk, hogy a sakktábla fekete és fehér figurái felcserélhetők egymással, és ehhez a cseréhez elég $2n\left(n+1\right)\cdot \left(n+2\right)$ lépés.   II. Most már csak az egy sorra vagy oszlopra vonatkozó állítást kell igazolnunk. Nyilván elég sorokra belátnunk az állítást, hiszen ebből ${90}^{\circ }$-os elforgatással már adódik az oszlopokra is. Tegyük fel, hogy valamely sorban a figurák jól helyezkednek el. A sor kívánt átrendezését $3$ részben hajtjuk végre, ez a $3$ rész kissé más, ha $n$ páratlan, és más, ha $n$ páros. Tekintsük tehát az alábbi $6$ helyzetet: $A:$ Az $1.$, $2.$, $\text{...}$, $n\mathrm{.}$ mezőn fekete, az $\left(n+2\right)\mathrm{.}$, $\left(n+3\right)\mathrm{.}$, $\text{...}$, $\left(2n+1\right)\mathrm{.}$ mezőn fehér figura áll, az $\left(n+1\right)$-edik mező üres;   $B:$ a páros mezőkön fekete, a páratlan mezőkön az első kivételével fehér figura áll, az első mező üres;   $B\text{'}:$ a páros mezőkön fehér, a páratlan mezőkön a $\left(2n+1\right)$-edik kivételével fekete figura áll, a $\left(2n+1\right)$-edik mező üres;   $C:$ a páros mezőkön fekete, a páratlan mezőkön a $\left(2n+1\right)$-edik kivételével fehér figura áll, a $\left(2n+1\right)$-edik mező üres;   $C\text{'}:$ a páros mezőkön fehér, a páratlan mezőkön az első kivételével fekete figura áll, az első mező üres;   $D:$ az $1.$, $2.$, $\text{...}$, $n\mathrm{.}$ mezőn fehér, az $\left(n+2\right)\mathrm{.}$, $\left(n+3\right)\mathrm{.}$, $\text{...}$, $\left(2n+1\right)$-edik mezőn fekete figura áll, az $\left(n+1\right)$-edik mező üres.   Azt kell belátnunk, hogy az $A$ helyzetből a $D$ helyzetbe el lehet jutni $n\left(n+2\right)$ lépésben. Ehhez a következőt fogjuk belátni: ha $n$ páratlan, akkor $A$-ból $B$-be és $C$-ből $D$-be $n\left(n+1\right)/2$ lépésben el lehet jutni, másrészt $B$-ből $C$-be $n$ lépés elég. Ez összesen $2\cdot n\left(n+1\right)/2+n=n\left(n+2\right)$ lépés. Páros $n$-re azt fogjuk belátni, hogy $A$-ból $B\text{'}$-be és $C\text{'}$-ből $D$-be $n\left(n+1\right)/2$ lépésben el lehet jutni, másrészt $B\text{'}$-ből $C\text{'}$-be $n$ lépés is elég. Páros $n$ esetén tehát $A$-ból $B\text{'}$ és $C\text{'}$-n keresztül lehet $n\left(n+2\right)$ lépésben $D$-be jutn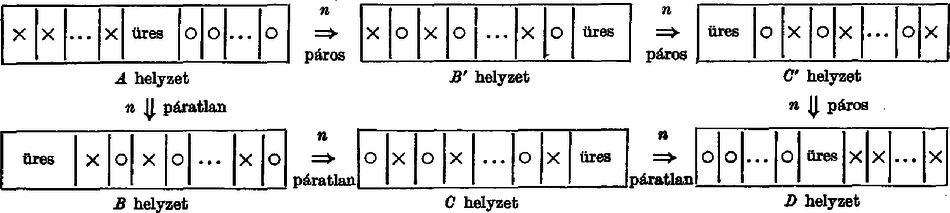i. Nézzük először, hogyan lehet $n$ lépésben $B$-ből $C$-be jutni! Ez egyszerű: az első lépésben a $3.$ mezőn álló figurával az $1.$ mezőre ugrunk, ezzel üresen marad a $3.$ mező, általában a $k$-adik lépésben a $\left(2k+1\right)$-edik mezőn álló figurával az üres $\left(2k-1\right)$-edik mezőre ugrunk és ezzel a $\left(2k+1\right)$-edik mező felszabadul. $B\text{'}$-ből $C\text{'}$-be hasonlóan lehet eljutni $n$ lépésben, csak most a páratlan mezőn álló figurákkal egyet-egyet jobbra kell ugrani és nem balra. Nyilvánvaló a következő is: $C$-ből pontosan annyi lépésben lehet $D$-be jutni, mint $D$-ből $C$-be (általában az egyik helyzetből a másikba ugyanannyi lépésben lehet eljutni, mint onnan vissza az elsőbe, csak a lépések sorrendjét kell megfordítani és minden lépést a fordítottjával kell helyettesíteni). Ha a $D$ és $C$ helyzetet a középső mezőre tükrözzük, éppen az $A$ és $B$ helyzetet kapjuk. Következésképp $A$-ból $B$-be ugyanannyi lépésben lehet eljutni, mint $D$-ből $C$-be vagy $C$-ből $D$-be. Ugyanígy lehet belátni, hogy $A$-ból $B\text{'}$-be ugyanannyi lépés elég, mint $C\text{'}$-ből $D$-be. Bizonyításunk befejezéséhez elég tehát azt megmutatnunk, hogy ha $n$ páratlan, akkor $A$-ból $B$-be, ha pedig $n$ páros, akkor $A$-ból $B\text{'}$-be $n\left(n+1\right)/2$ lépésben el lehet jutni. Erre egy eljárást fogunk megadni, az eljárás $n$ "szakaszból'', azon belül a $k$-adik "szakasz'' $k$ lépésből fog állni: 1. szakasz: az $n$-edik mezőn álló (fekete) figurát egy mezővel jobbra toljuk; 2. szakasz: az $\left(n+2\right)$-edik mezőn álló (fehér) figurával balra ugrunk (az $n$-edik mezőbe), majd az $\left(n+3\right)$-adik mezőn álló (fehér) figurát egy mezővel balra toljuk; 3. szakasz: most már két fekete figurával tudunk jobbra ugrani (előbb az $\left(n+1\right)$-edik mezőről az $\left(n+3\right)$-adikra, majd az $\left(n-1\right)$-edik mezőről az $\left(n+1\right)$-edikre), ezután az $\left(n-2\right)$-edik mezőn álló fekete figurát eggyel jobbra toljuk stb. A $k$-adik szakasz után a sor (az üres mezőt figyelmen kívül hagyva) $3$ "tömbből'' áll: az első "tömb'' $n-k$ darab fekete figurából, a második "tömb'' $k$ figurapárból áll, a pár első figurája mindig fekete, a második mindig fehér. A harmadik "tömb'' $n-k$ fehér figurából áll. Ha $k$ páratlan, akkor az üres mező az $1.$ és a $2.$ tömb között van a $k\mathrm{.}$ szakasz után; ha $k$ páros, akkor az üres mező a $2.$ és a $3.$ tömb között van a $k\mathrm{.}$ szakasz után. 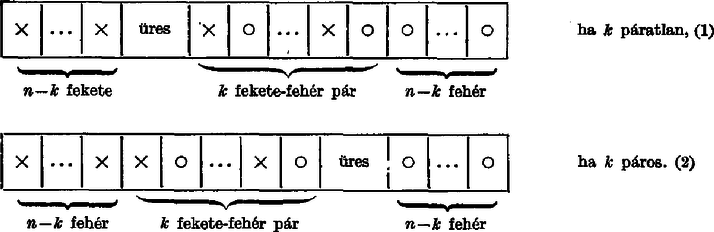Az első esetben ($k$ páratlan) ugorjunk a $2.$ tömb fehér bábuival egyet-egyet balra! Ezt megtehetjük, ha a tömb legbalra álló figurájával kezdjük. Így az üres mező végül az $\left(n+k+1\right)$-edik mezőre kerül. Toljuk most át erre a mezőre a $3.$ tömb bal szélén álló figurát. Ez a $k+1$ lépés alkotja a $\left(k+1\right)$-edik szakaszt. A $\left(k+1\right)$-edik szakasz után tehát így alakul a helyzet: Ez valóban $\left(2\right)$ alakú. A második esetben (ha $k$ páros, $k+1$ páratlan), a $2.$ tömb fekete bábuival ugrunk egyet-egyet jobbra, (ezt a tömb legjobbra álló fekete figurájával kell kezdeni), majd az $1.$ tömb jobb szélső figuráját toljuk az így megüresedő $\left(n-k+1\right)$-edik helyre. Ez a $k+1$ lépés alkotja a $\left(k+1\right)$-edik szakaszt, eredményeként egy $\left(1\right)$ alakú sort kapunk. Végül az $n$-edik szakasz végrehajtása után az $1.$ és a $3.$ tömb kiürül. Ha $n$ páratlan, akkor az üres mező az $n$ fekete-fehér pár előtt áll, ami éppen a $B$ helyzet. Ha $n$ páros, akkor az üres mező az $n$ fekete-fehér pár után fog állni, ami a $B\text{'}$ helyzet. A $k$-adik szakaszban pontosan $k$ lépést ($k-1$ ugrást és egy tolást) hajtottunk végre, és eljárásunk $n$ szakaszból állt, így eljárásunkhoz $1+2+\text{...}n=n\left(n+1\right)/2$ lépésre volt szükség. Ezzel bebizonyítottuk, amit akartunk.   (S. L.)   Megjegyzés. Megadtunk egy algoritmust, amivel a fekete és fehér figurákat $2n\left(n+1\right)\left(n+2\right)$ lépésben felcserélhetjük. Megmutatjuk, hogy a helycsere elvégzéséhez $2n{\left(n+1\right)}^2$ lépésre mindenképpen szükség van, ennél kevesebbel semmilyen eljárással sem jutunk célhoz. Tekintsük ehhez azt a fekete figurát, amelyik az $i$-edik sor és a $j$-edik oszlop kereszteződésében áll. A cserék végrehajtása után egy fehér figura helyére, mondjuk az $f\left(i\mathrm{,}j\right)$-edik sor és a $g\left(i\mathrm{,}j\right)$-edik oszlop kereszteződésébe került. Mivel a figurák csak vízszintesen és függőlegesen tudnak mozogni, s egy lépésben legfeljebb $2$ mezővel kerülnek odább, azért a kiszemelt figurával legalább $\begin{array}{c}{\displaystyle \frac{|f\left(i\mathrm{,}j\right)-i|}{2}+\frac{|g\left(i\mathrm{,}j\right)-j|}{2}}\end{array}$ lépést kellett tennünk. Az összes fekete figurával tehát együttvéve legalább lépést kellett tennünk. Itt a $\sum$ jel alatt álló $\left(i\mathrm{,}j\right)$ pár a fekete figurák kezdeti helyein fut végig, $\left(f\left(i\mathrm{,}j\right)\mathrm{,}g\left(i\mathrm{,}j\right)\right)$ pedig a helycsere végén elfoglalt helyüket mutatja, vagyis az $\left(f\left(i\mathrm{,}j\right)\mathrm{,}g\left(i\mathrm{,}j\right)\right)$ pár éppen a fehér figurák kezdeti helyein fut végig. Ezért a ${\sum }_{\left(i\mathrm{,}j\right)}i$ összegben az $1$ és $\left(n+1\right)$ közötti egészek $n$-szer, az $\left(n+2\right)$ és $\left(2n+1\right)$ közöttiek $\left(n+1\right)$-szer fordulnak elő, míg a ${\sum }_{\left(i\mathrm{,}j\right)}f\left(i\mathrm{,}j\right)$ összegben az $1$ és $n$ közötti egészek $\left(n+1\right)$-szer, az $\left(n+1\right)$ és $\left(2n+1\right)$ közöttiek pedig $n$-szer találhatók meg. A $\left(*\right)$ egyenlőtlenség jobb oldalán az első tag kétszerese tehát $\begin{array}{c}{\displaystyle \left[\left(n+2\right)+\text{...}+\left(2n+1\right)\right]-\left[1+2+\text{...}+n\right]=n\left(n+1\right)\mathrm{.}}\end{array}$ Hasonlóan kapjuk, hogy a második tag kétszerese $\begin{array}{c}{\displaystyle \left(2n+1\right)\left[\left(n+2\right)+\text{...}+\left(2n+1\right)-\left(1+2+\text{...}+n\right)\right]=\left(2n+1\right)n\left(n+1\right)\mathrm{.}}\end{array}$ Így a fekete figurákkal tett lépések száma legalább $\begin{array}{c}{\displaystyle \frac{1}{2}\left[n\left(n+1\right)+\left(2n+1\right)n\left(n+1\right)\right]=n{\left(n+1\right)}^2\mathrm{.}}\end{array}$ A fehér figurákkal is legalább ennyit kell lépnünk, ami éppen az állított $2n{\left(n+1\right)}^2$ lépést jelenti.