Feladat: Gy.1622 Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Csapó Ildikó 
Füzet: 1976/november, 146 - 148. oldal  PDF  |  MathML 
Témakör(ök): Sík parkettázás, Négyzetek, Gyakorlat
Hivatkozás(ok):Feladatok: 1976/február: Gy.1622

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat 8-féle felosztást követel. Ennek még úgy is eleget lehet tenni, ha a falrész valamelyik átlójára szimmetrikus felosztásokra szorítkozunk; sőt még azt is előírhatta volna a fáraó, hogy a tengelynek választott átlót pontosan 2 kisebb négyzet fedje le. Ezek a többletkövetelmények csökkentik ugyan a javasolható megoldások számát, de még marad elég, másrészt így bizonyos egységet vihetünk a keresésbe.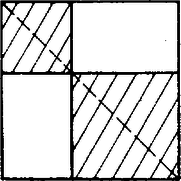
Az első két ‐ majd ezután kiadódó oldalú ‐négyzetnek egy csúcsa közös (1. ábra).

 

 

1. ábra
 

A fennmaradó két egybevágó téglalapot együtt 8, tehát egyenként 4 négyzetre kell bontanunk. Fordítsuk meg a feladatot, és vizsgáljuk: hogyan, hányféleképpen rakhatunk össze 4 négyzetből téglalapot. Erre a 2. ábra 5 lehetőséget mutat: egybevágó négyzetekből kettőt: A és B, két különböző méretűből szintén kettőt: C(2:2) és D(1:3), végül három különböző oldalúból egy lehetőséget (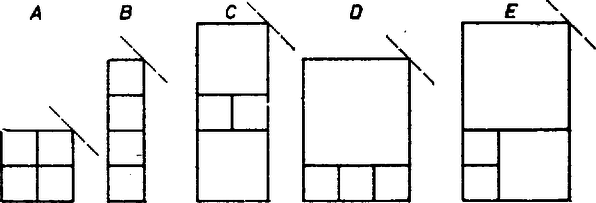E).
 

 

2. ábra
 

Ha most mindegyik összeállítást tükrözzük a jobb felső csúcsánál levő külső szögek felezőjére, majd a 8 négyzetből álló alakzatot egy négyzetbe foglaljuk bal és jobb szélső, valamint alsó és felső határvonalának meghosszabbításával, máris 5 megoldásunk van (3‐7. ábrák bal oldali része).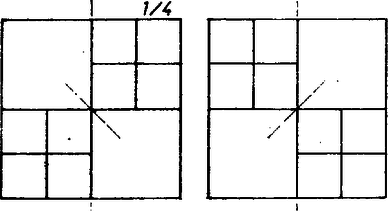
 

 

3. ábra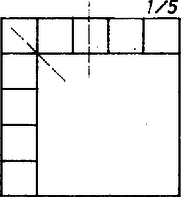
 

 

 

4. ábra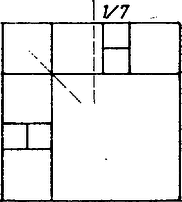
 

 

 

5. ábra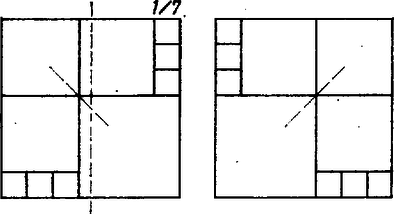
 

 

 

6. ábra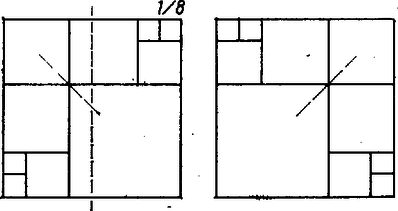
 

 

 

7. ábra
 

Belátjuk, hogy e felbontásokban nem fordul elő kétszer ugyanaz a kis négyzet. A nagy négyzet oldalait a felhasznált osztó vonalak és meghosszabbításaik az egyes ábrákon rendre az oldal 14,15,17,17,18, részében metszik, így közös osztóvonalról csak a 3. és a 7. ábrán, valamint az 5. és 6. ábrán lehet szó, de a finomabb összehasonlítás mutatja, hogy közös négyzet ezekben a párokban sincs.
A hátra levő 3 megoldást kiadja a 3., 6, és 7. ábrának a függőleges középvonalra való tükörképe (az illető ábrák jobb oldali része), könnyű látni, hogy az eddigi 8 felbontás együttesen megfelel a fáraó követelményének. (A 4. és 5. ábra tartalmaz tükrösen egybevágó résznégyzeteket.) ‐ Állításunk bizonyítását befejeztük.
 

  Csapó Ildikó (Sopron, Széchenyi I. Gimn., III. o. t.)
 

Megjegyzések. 1. Többféleképpen is kaphatunk további felosztásokat: a) a C ábrán a két kis négyzetet a téglalap szélére toljuk; b) D,E és az új C helyett valamelyik szimmetrikus képüket vesszük; c) feladjuk a két téglalap tengely szimmetrikus kitöltését, d) a 3. ábra helyett a 8. ábrát használjuk;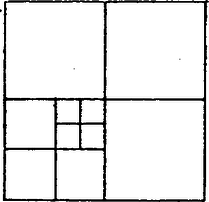
 

 

8. ábra
 

e) feladjuk az átlónak csak 2 négyzettel való lefedését (9. ábra).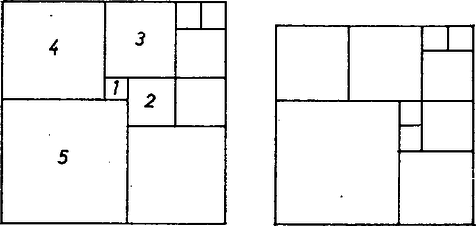
 

 

9. ábra
 

‐ Hangsúlyozzuk azonban, hogy ez csak előkészítés a feladat teljes megoldásához.
2. Számos hasonló érdekes felosztási problémával foglalkoznak a matematikusok. Az érdeklődőknek ajánljuk Gallai Tibor cikkét az Élő matematika I. (Tankönyvkiadó, Budapest, 1968) c. gyűjteményben.
3. Feladatunk konkrét elődje az 1973. évi Arany Dániel kezdők verseny I. fordulójának 7. feladata: Bizonyítsuk be, hogy ha n>5, akkor a négyzet felbontható az oldalaival párhuzamos vágásokkal n darab négyzetre.