Feladat: Gy.1621 Korcsoport: 14-15 Nehézségi fok: könnyű
Füzet: 1976/november, 145 - 146. oldal  PDF  |  MathML 
Témakör(ök): Lefedések, Szimmetrikus sokszögek, Gyakorlat
Hivatkozás(ok):Feladatok: 1976/február: Gy.1621

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A válasz igenlő. Képezzünk a 20 db érméből négyes csoportokat a következő módon: először lerakunk az asztalra 3 darab egymást kölcsönösen érintő érmét, majd a negyediket úgy, hogy az előző három közül pontosan kettőt érintsen. Így a négy érme közül kettő másik hármat, kettő pedig másik kettőt érint.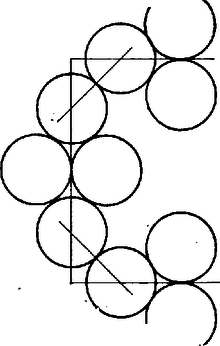
Az így nyert négyes csoportokat egymás mellé helyezhetjük a feltételnek megfelelően, ha a továbbiakban mindig azt a két érmét fektetjük egymás mellé, amelyik pontosan másik kettőt érint az előzőek közül, és ügyelünk arra, hogy a kör bezáruljon.

 

 

Ezt mindig elérhetjük; öt négyes csoport esetén például úgy, hogy egy szabályos ötszöget rakunk ki.
Jelöljük a k1,k2,k3,k4 körök középpontjait rendre O1,O2,O3,O4-gyel, ahol O1O3 annak a két körnek a középpontját köti össze, amelyik 2‐2 másik kört érint.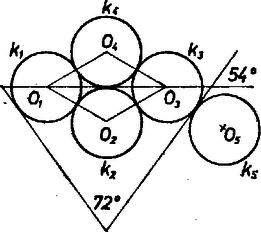
 

 

A k3-hoz csatlakozó k5 körnek a k3-mal közös belső érintője az O1O3 egyenessel 54∘-os szöget zár be, mivel az ötszög szabályos.
Az O1O2O3O4 pontok egy rombusz csúcsai, és O1O3O4∢=30∘. A k3,k4 körök közös külső érintője is 30∘-os szöget zár be az O1O3 centrálissal (a tengelyes szimmetria miatt ugyanúgy a k1,k4 érintője is), amiből következik, hogy a k1,k2,k3,k4 körök mindegyike az 54∘-os egyenesek szögtartományán belül halad, azaz a csatlakozó négyes csoporttal csak egy érintkezési pontja lehet és van is.
 

Megjegyzés. Ugyanígy kirakhatunk a feltételnek megfelelően minden 12-nél több, 4-gyel osztható számú érmét.
Tizenkettőnél már bekövetkezik az, amit a megoldásunkban 20-nál még ki tudtunk zárni, hogy a belső körök között is van egy nem kívánt érintkezés.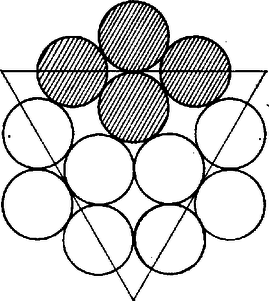