Feladat: 1598. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1977/október, 68 - 69. oldal  PDF  |  MathML 
Témakör(ök): Egyenes, Kör (és részhalmaza), mint mértani hely, Húrnégyszögek, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):Feladatok: 1975/október: 1598. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel az AC, BD szakaszok metszik egymást, ABCD konvex négyszög. Ha M vetületei az oldalszakaszokon vannak, PQRS is konvex, és az MP, MQ, MR, MS szakaszok a négyszög belsejében vannak. Megmutatjuk, hogy ezek rendre felezik a PQRS négyszög szögeit. Esetünkben például az MB szakasz elválasztja a P, Q pontokat, és ezekből derékszög alatt látszik. Emiatt PBM∢=PQM∢. Az MC szakasz a Q, R pontokat választja el, és ezekből látszik derékszög alatt. Így MQR∢=MCR∢. Mivel pedig a PBM∢ az ABD∢-gel MCR∢ pedig ACD∢-gel azonosak, és az utóbbiak egyenlőek, PQM∢ valóban egyenlő MQR∢-gel. M tehát a PQRS négyszög szögfelezőinek a metszéspontja, így egyenlő távolságra van az oldalaktól.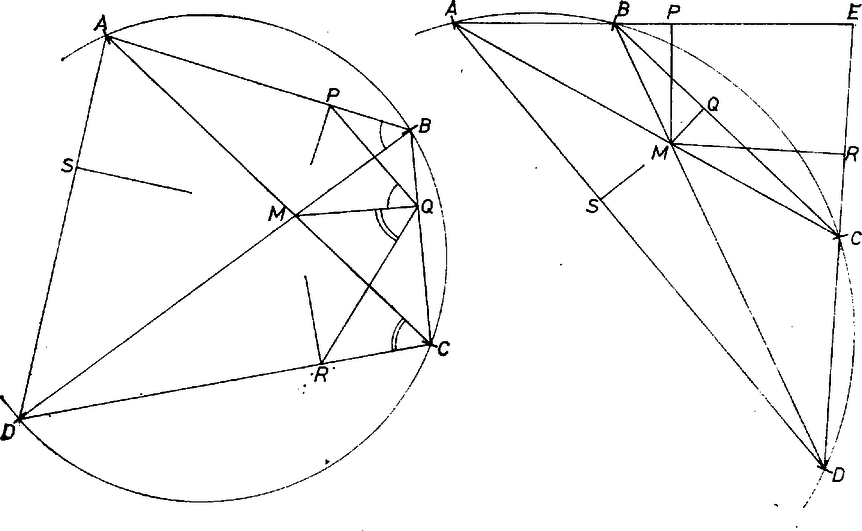

 

 

Az eddig vizsgált eset akkor fordul elő, ha az ABCD négyszög oldalai a csúcsokból hegyes szög alatt látszanak. Ha például AD a B, C csúcsokból tompa szög alatt látszik, az AB, DC félegyenesek metszik egymást, jelöljük a metszéspontjukat E-vel. Ekkor a Q, S pontok továbbra is a BC, AD szakaszokon lesznek, de a P, R pontok a BE, CE szakaszokra kerülnek. A PQRS négyszög Q-nál levő szöge konkáv, és MQ épp arra a két tompaszögre vágja szét, amely alatt AD a B, C csúcsokból látszik. Most ugyanis P és Q az MB szakasznak ugyanazon az oldalán vannak, tehát PQM∢ a PBM∢ mellékszögével egyenlő. Ez azonban nem más, mint az ABD∢, és hasonlóan kapjuk, hogy MQR∢=ACD∢.
Az, hogy az MR, MS, MP egyenesek felezik a PQRS négyszög szögeit, ugyanúgy látható be, mint az első esetben. M tehát most is a szögfelezők metszéspontja, így tőle a négyszög oldalai egyenlő távolságra vannak.