Feladat: 1586. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: -
Füzet: 1976/november, 140 - 141. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Terület, felszín, Szimmetrikus alakzatok, Gyakorlat
Hivatkozás(ok):Feladatok: 1975/május: 1586. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Könnyen belátható, hogy A és B nem lehet egy átmérő két végpontja. Ha ez teljesül, akkor bármilyen AB körív teljes egészében az AB által meghatározott valamelyik félkör belsejében haladna, tehát a területet nem felezhetné, (A felező az átmérő lenne, amely ,,végtelen sugarú'' körívnek tekinthető, de itt ilyen köröket nem értelmezünk.)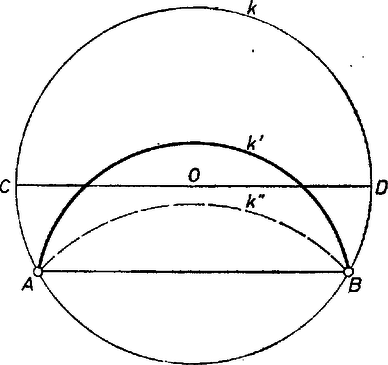
Belátható az is, hogy ha AB<d(d az átmérő), akkor a k kör O középpontja az AB húr és a k' között van.
 

 

1. ábra
 

Tegyük fel ugyanis, hogy ennek az ellenkezője igaz, vagyis k'' ív és az AB húr által határolt tartomány nem tartalmazza O-t. Húzzuk meg az AB-vel párhuzamos CD átmérőt, k'' ekkor teljes egészében az AB-t tartalmazó félkörben halad, vagyis a két AB körszelet területösszege kisebb a CD félkör területénél, tehát k'' nem felezhet.
Húzzuk meg az AB húr m felező merőlegesét, m és k' metszéspontja F, m talppontja AB-n T. ATO derékszögű háromszög, tehát AOF∢ tompaszög, így az AOF háromszögben a legnagyobb oldal a vele szemben fekvő 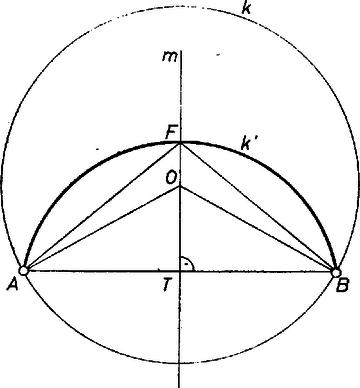AF.
 

 

2. ábra
 

A fentiek alapján
AF>AO=d/2.
Nyilvánvaló, hogy k' ív AF darabja hosszabb az AF egyenes szakasznál, így AF⌢(k')>AF>d/2. Mivel az ábra szimmetrikus, AB⌢(k')>2⋅d/2=d.
Érdekes megjegyezni, hogy a bizonyítás arra a határesetre is érvényes, amikor A és B egybeesik, ekkor m az A-beli sugár egyenese, és AOF∢=180∘.