Kezdőlap


Feladat:	1569. matematika gyakorlat	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1976/március, 109 - 111. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Mértani helyek, Térbeli ponthalmazok távolsága, Térelemek és részeik, Gyakorlat
Hivatkozás(ok):	Feladatok: 1975/február: 1569. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A feladat feltételeit természetesen úgy értelmezzük, hogy a négy sík közt nincs további (ki nem mondott) párhuzamossági kapcsolat; vagyis pl. $L_{1}$ metszi az $L_{3}$ -at, így persze $L_{2}$ is metszi, másrészt $L_{1}$ és $L_{2}$ az $L_{4}$ -et is metszik, hiszen ha két párhuzamos sík egyike átmetsz egy harmadik síkot, akkor azt a pár másik síkja is átmetszi. Ekkor a négy, páronkénti metszési egyenes párhuzamos egymással; jelöljük $L_{1}$ és $L_{3}$ közös egyenesét $m$ -mel.
2. Feladatunkat visszavezetjük egy síkbeli feladatra, a következő észrevétel alapján. Ha egy $P$ pont hozzátartozik a keresett $H$ mértani helyhez (ponthalmazhoz), akkor a $P$ -n átmenő, $m$ -mel párhuzamos $m_{p}$ egyenes minden pontja $H$ -hoz tartozik. Valóban, $m_{p}$ az $m$ közvetítésével párhuzamos $L_{1}$ -gyel és $L_{3}$ -mal, és ekkor $L_{2}$ -vel, illetve $L_{4}$ -gyel is, így $m_{p}$ minden egyes pontjának a négy síktól mért távolságai rendre ugyanakkorák, mint $P$ megfelelő távolságai. Ennek alapján elég megkeresni $H$ pontjait egy, a $P$ -n átmenő, az $m$ -mel nem párhuzamos síkban.

Ezt az

S

síkot mi az

m

-re merőlegesnek vesszük, így

P

-nek az

L_{i}

síktól mért távolsága

(i = 1, 2, 3, 4)

rendre egyenlő az

S

és

L_{i}

közös

e_{i}

egyenesétől mért

d_{i}

távolságával, hiszen

S

megválasztása alapján

P

-nek

L_{i}

-n és

e_{i}

-n levő vetülete azonos. És most

S

-ben azon pontok

H_{S}

mértani helyét fogjuk keresni, amelyekre nézve

\begin{matrix} d_{1} + d_{2} + d_{3} + d_{4} = c, \end{matrix}

ahol

c

az eredetileg adott szám.

3. Tudjuk ehhez, hogy

e_{1} ∥ e_{2}

és

e_{3} ∥ e_{4}

, tehát e négy egyenes egy paralelogrammát zár körül és az

S

-en 8 további részt hoz létre (közös belső pont nélküli részek, 1. ábra), 4 szögtartományt ‐ amelyeket egy‐egy félegyenes határol ‐ és 4 fél síksávot, határaik két‐két félegyenes és a paralelogramma egy‐egy oldalszakasza.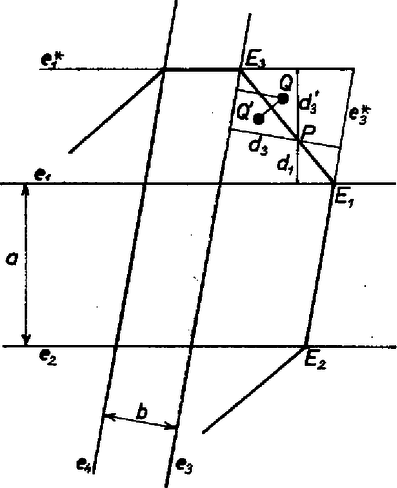

1. ábra

Tovább redukálhatjuk feladatunkat: elég

H_{S}

pontjait megkeresni a paralelogrammában, a szögtartományok egyikében és a fél síksávok egyikében, hiszen problémánk nem változik meg sem az 1 és 2, sem a 3 és 4 indexek fölcserélésével, sem akkor, ha e két cserét egyszerre hajtjuk végre. Válasszuk azt a fél síksávot (I.), amelyben

d_{3} < d_{4}

és azt a szögtartományt, amelyben ezen felül még

d_{1} < d_{2}

teljesül (II.), másrészt jelöljük

e_{1}

és

e_{2}

távolságát

a

-val,

e_{3}

és

e_{4}

távolságát

b

-vel. (Az utóbbiak egyszersmind

L_{1}

és

L_{2}

, illetve

L_{3}

és

L_{4}

távolságát is jelentik.)

4. A két‐két párhuzamos közti pontokra

d_{1} + d_{2} = a

, illetve

d_{3} + d_{4} = b

(beleértve az egyik‐egyik párhuzamoson levő pontokat is), ezért a paralelogramma minden belső és kerületi pontjára, csúcsára a 4 távolság összege

a + b

. Eszerint

c = a + b

esetén az egész paralelogramma a

H_{S}

-hez tartozik,

c \neq a + b

esetén pedig egy pontja sem tartozik hozzá.
Az I. félsávban és a II. részben

d_{4} = d_{3} + b

, így

d_{3} + d_{4} = 2 d_{3} + b \geq b

, a II. tartományban ezen felül, hasonlóan

d_{1} + d_{2} = 2 d_{1} + a \geq a

, és egyenlőség csak az

e_{3}

-nak, illetve az

e_{1}

-nek a határvonalakon figyelembe vett pontjaira teljesül.
Ezek szerint

c = a + b

esetén

H_{S}

-hez a félsávokból és a szögtartományokból nem tartozhat belső pont;

c < a + b

esetén

H_{S}

üres ponthalmaz;

c > a + b

esetén pedig

H_{S}

-hez csak a paralelogrammán kívüli pontok tartozhatnak, mégpedig az I.-ből és a II.-ből csak azok, amelyekre teljesül az I.-ben:

\begin{matrix} d_{1} + d_{2} + d_{3} + d_{4} = a + b + 2 d_{3} = c, \end{matrix}

a II.-ben:

= 2 d_{1} + a + 2 d_{3} + b = c

,
vagyis az I.-ben:

\begin{matrix} d_{3} = \frac{1}{2} (c - a - b) = c', \end{matrix}

a II.-ban:

\begin{matrix} d_{1} + d_{3} = c' . \end{matrix}

Az első követelmény csak abból az

e_{3}^{*}

egyenesből az I.-be eső

E_{1} E_{2}

szakasznak a pontjaira teljesülhet, amely

e_{3}

-tól

c'

távolságban halad, és ezekre nyilvánvalóan teljesül is.
Legyen hasonlóan

e_{1}^{*}

e_{1}

-től

c'

távolságban (a II.-on át) haladó egyenes, továbbá legyen ennek

e_{3}

-on levő pontja

E_{3}

. Ekkor a második követelménynek a II. határvonalán megfelelnek

E_{1}

és

E_{3}

, és a belsejében az

E_{1} E_{3}

szakasz pontjai. Ugyanis

e_{1}

e_{3}^{*}

e_{1}^{*}

és

e_{3}

egy rombusz oldalegyenesei,

E_{1} E_{3}

ennek átlója, tehát szimmetriatengelye is, az

E_{1} E_{3}

-ra való tükrözés

e_{3}

-at

e_{1}^{*}

-ba viszi át, így az átlószakasz belső

P

pontjaira

d_{3}

egyenlő

P

-nek

e_{1}^{*}

-tól mért távolságával,

d_{1} +

+ d_{3} = c'

. Ha viszont egy

Q

pont nincs rajta a tengelyen, akkor

e_{3}

-tól és

e_{1}^{*}

-től mért távolságai nem egyenlők, tehát

d_{1} + d_{3} \neq c'

, ilyen pont nem tartozhat

H_{S}

-hez.
Ezek szerint

c > a + b

esetén

H_{S}

a 8 síkrész egy‐egy szakaszából áll össze (az egyenesek indexeinek fent említett cseréivel.) E szakaszok végpontjai, egyben páronkénti csatlakozási pontjai

e_{1}

-en és

e_{2}

-n az

e_{3}

-tól és az

e_{4}

-től

c'

-re levő pontok,

e_{3}

-on és

e_{4}

-en pedig az

e_{1}

-től és az

e_{2}

-től

c'

-re levő pontoknak.
A keresett

H

-t pedig

c > a + b

esetén így kapjuk:

E_{1}

-en át vesszük az

L_{1}

és

L_{3}

közös

m

egyenesével párhuzamos egyenest és ezt körültoljuk

H_{S}

8 szakaszán, míg újra áthalad

E_{1}

-en, a mozgó egyenes 8 síksávot ír le (2. ábra).

2. ábra

c = a + b

esetben pedig

H

az a hasábos (végtelenbe nyúló) térrész, melyet a négy adott sík közrezár, beleértve ennek a határpontjait is.

Megjegyzés. Ha megengedjük, hogy

L_{1}

és

L_{3}

párhuzamosak lehessenek, akkor tisztáznunk kell a 4 (különböző) sík sorrendjét és ismernünk kell szomszédos páronkénti távolságaikat is. Ekkor

c

értéke szerint

H

vagy üres ponthalmaz, vagy a két közbülső sík közti térréteg, vagy pedig két sík, amelyek közül az egyik vagy mind a kettő azonos is lehet valamelyik szélső síkkal.