Feladat: 1561. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: -
Füzet: 1976/január, 17 - 19. oldal  PDF  |  MathML 
Témakör(ök): Körülírt kör, Magasságpont, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1975/január: 1561. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Ismeretes, hogy az M magasságpontnak mindhárom oldalegyenesre való tükörképe rajta van a háromszög köré írt k körön. Ezért M-nek AC-re való Mb tükörképe azonos B'-vel, hiszen így MMb⊥AC⊥MB, és M-en át csak egy merőleges van AC-re, másrészt MB és k közös pontjai B és B'. Ugyanígy C' az M-nek AB-re való tükörképe. Eszerint B'A=MA=C'A, vagyis B', C' és M egy A középpontú k1 körön vannak rajta. E kör két húrja 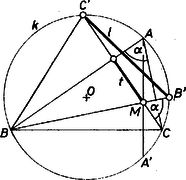C'B'=l és C'M=2t.
2. Megmutatjuk, hogy az AB'C' egyenlő szárú háromszög A-nál levő szöge 2⋅BAC∢=2α, illetve 2(180∘-α) aszerint, hogy α hegyesszög, illetve tompaszög. Ennek alapján A, majd k1 az l-ből és α-ból megszerkeszthető, és rajta M kijelölhető lesz, továbbá B', C', A meghatározza k-t, és ebből MB' kimetszi B-t, MC' pedig C-t.
Egy konkrét háromszögből kiindulva, k1 révén a B'AC' középponti szög kétszer akkora, mint vagy a B'MC' kerületi szög, vagy ennek a kiegészítő szöge aszerint, hogy M a B'C' egyenesnek az A-t tartalmazó partján van, illetve a másik partján. Továbbmenve, a B'MC' szög mindenképpen egyenlő a BMC szöggel, mert ha M kívül adódik k-n, akkor e két szög azonos, ha pedig M a k-ban van, akkor egymás csúcsszögei, hiszen M a BB' és CC' húrok közös pontja. M-nek k-hoz képest külső, illetve belső helyzete ‐ mint ismeretes ‐ azon múlik, hogy van-e tompaszög az ABC háromszög szögei közt, vagy nincs. (Derékszögű háromszögben M azonos a derékszög csúcsával.) Tekintsük külön-külön az eseteket.
Hegyesszögű háromszögben B'MC'∢=BMC∢=BA'C∢=180∘-BAC∢=180∘-α, ahol A' az M-nek BC-re való tükörképe (1. ábra).

 

 

1. ábra
 

Másrészt B'C' elválasztja A-t M-től, hiszen ekkor B' a B-t nem tartalmazó AC íven van, C' a C-t nem tartalmazó AB íven, vagyis a pontok sorrendje C,B', A,C', B, és M a CC'BB' szakaszok közös pontja. Így a fentiek szerint
B'AC'∢=2(180∘-B'MC'∢)=360∘-2BMC∢=2α.

Tompaszögű háromszögben, ha α hegyesszög, választhatjuk úgy a betűzést, hogy β>90∘, hiszen a B és C, illetve B' és C' pontok szerepe feladatunk szempontjából egyező (2. ábra).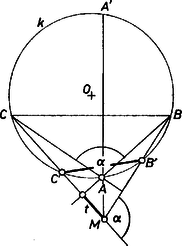
 

 

2. ábra
 

Ekkor B' az MCC' egyenesnek B-t tartalmazó partján van,
B'MC'∢=90∘-MCA∢=BAC∢=α,
tehát ekkor is B'AC'∢=2α. ‐ Ha viszont α>90∘, akkor M az AA'-nek A-n túli meghosszabbításán van, vagyis B'C'-nek A-t tartalmazó partján (3. ábra), így
B'AC'∢=2⋅B'MC'∢=2⋅BA'C∢=2(180∘-BAC∢)=2(180∘-α).
 

 

3. ábra
 

Ezzel állításunk bizonyítását befejeztük, a szerkesztés egy lehetséges végrehajtását pedig már fönt vázoltuk.
A végrehajtásból kiküszöbölhetjük az α hegyes- vagy tompaszög voltából adódó vagylagosságot. Fölvesszük a B'C'=l szakasz helyzetét, és C' körül 2t sugárral k2 kört írunk. B'C'-re a végpontjaiban egyirányú merőleges félegyeneseket állítunk. Ezeket B', illetve C' körül egymás felé elfordítjuk α-val, metszéspontjuk adja A-t, majd még egyszer α-val, ezek metszéspontja O, a k középpontja. Megrajzoljuk k1-et, ez a k2-t a magasságpont lehetséges M1, M2 helyzeteiben metszi, majd k-t, ez MiB'-ből B-t, MiC'-ből C-t metszi ki, ahol i=1,2. Amennyiben a BAC szög (180∘-α)-nak adódik, az a megoldás nem felel meg.
A szerkesztés helyességének belátását az olvasóra hagyjuk.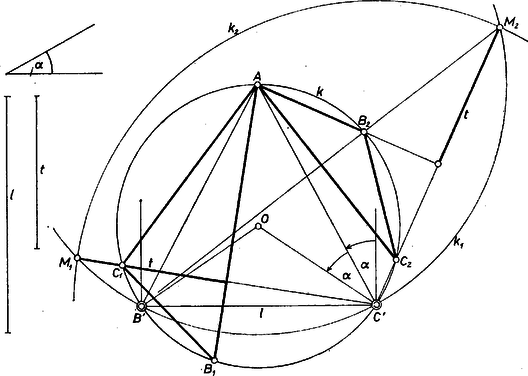
 


 

Az előírt méretek között a megoldást biztosító nagyságviszonyokat pontosan egy egyszerű trigonometriai számítás adhatná meg. Külön megemlítjük az α=90∘ esetet. Ebből adódik, hogy csak l=0 és t=0 lehet, különben az adatrendszer ellentmondó; ha viszont l=t=0, akkor tetszőleges derékszögű háromszög megfelel, tehát ez az adatrendszer határozatlan. Külön-külön is szükséges, hogy l≠0 és t≠0. A fent leírt szerkesztésben az elsőként felhasznált l-re természetesen nincs korlátozás, t-re viszont felső korlátot szab, hogy nem lehet nagyobb C'A-nál.