Kezdőlap


Feladat:	1555. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1976/január, 15 - 17. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Beírt alakzatok, Forgatva nyújtás, Diszkusszió, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1974/december: 1555. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A kívánt téglalap $E F G$ részháromszöge derékszögű, és az $E G = 2 \cdot E F$ követelmény szerint hasonló a tengelye mentén kettévágott szabályos háromszög feléhez. Ezért az $E G$ átló a végpontjainál levő derékszögeket $30^{\circ}$ -os és $60^{\circ}$ -os részekre, vagyis $1 : 2$ arányban osztja.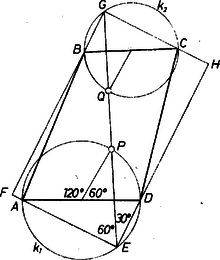
Az $E$ csúcs csak az $A D$ szakasz $k_{1}$ Thalész-körén lehet ‐ ha egyáltalán van megoldása a feladatnak ‐, pontosabban az $A D$ -nek a $B$ -t és $C$ -t nem tartalmazó partján levő félkörön, hasonlóan $G$ a $B C$ átmérőjű $k_{2}$ körnek csak azon a félkörén lehet, amelyet $B C$ elválaszt $A$ -tól (1. ábra).

1. ábra

Jelöljük az

E G

egyenesnek

k_{1}

-en levő második (azaz

E

-től különböző) metszéspontját

P

-vel, a

k_{2}

-n levőt

Q

-val. Ekkor a

D P

és a

P A

, valamint a

B Q

és a

Q C

ívek aránya is

1 : 2

, mert egy körben két ív aránya egyenlő a rajtuk álló középponti szögek arányával, és így a kerületi szögek arányával is. Eszerint

P

harmadolja azt a

D A

félkört, amelyik

A D

-nek a

B

-t tartalmazó (röviden: belső) partján van, és

Q

harmadolja a belső

B C

félkört. Eszerint

P

és

Q

kimetszhetők a

D

körüli

D A / 2

, illetve a

B

körüli

B C / 2

sugarú körrel, ezután a

P Q

egyenes

k_{1}

-ből,

k_{2}

-ből kimetszi

E

-t,

G

-t, és a keresett téglalap oldalegyeneseire csak az

E A

E D

G B

G C

egyenesek jönnek szóba.
Az így kapott

E F G H

négyszög oldalegyenesei az előírás szerint rendre átmennek az adott

A

B

C

D

pontokon, az

E

-ben és a

G

-ben összefutó

2 - 2

egyenes Thalész tétele alapján merőleges egymásra, végül

E H | | F G

, mert az

E D

G B

félegyenesek egyenlő (

30^{\circ}

-os) szöggel hajlanak

E G

-hez ennek két partján, tehát váltószögek, és ugyanígy

E F | | G H

. Így a kapott

E F G H

négyszög mindenesetre a kívánt arányt mutató téglalap. Azt viszont csak a szerkesztés végrehajtása után lehet eldönteni, megfelel-e annak a szigorúbb követelménynek, hogy az

A

B

C

D

pont a téglalapnak rendre a megfelelő oldalszakaszán legyen rajta.
A két kör és rajta

P

, illetve

Q

kijelölése egyértelműen lehetséges, így a szerkesztés végrehajthatósága csak azon múlik, hogy

P

és

Q

különböző pontok-e, alkalmasak-e egy egyenes meghatározására. Ha

Q

egybeesik

P

-vel, akkor az

E G

egyenes tetszőlegesen választható, úgy, hogy egyik-egyik félegyenese az

A P D

, illetve a

B P C

szögtartományban haladjon.

Megjegyzések. 1. Ajánljuk az olvasónak, vázoljanak a kívánt téglalaphoz olyan

A B C D

kiindulási négyszögeket, amelyeknek

1

csúcsa egy meghosszabbításra esik, majd

2

3

4

csúccsal ez a helyzet. Ilyen "visszafelé való spekulációval'' (helyzetek elemzésével) is szoktathatnák magukat a feladatok végén szükséges diszkusszióra. Keressenek olyan

B

C

-t is a megválasztott

A

D

pontpárhoz, amelyre

Q

egybeesik

P

-vel!
2. A dolgozatok nem tartalmaztak diszkussziót.
3. A megoldás a következő, sokszor felvetett feladatnak a mintájára készült: olyan négyzet szerkesztendő, amelynek oldalai (oldalegyenesei) előírt sorrendben átmennek

4

előre megadott ponton.

II. megoldás. Húzzunk

A

-n át

B D

-re merőleges egyenest és jelöljük a keresett

G H

egyenesen levő pontját

A_{1}

-gyel, továbbá,

A_{1}

-nek

E F

-en,

B

-nek

E H

-n levő vetületét rendre

A'_{1}

-vel,

B'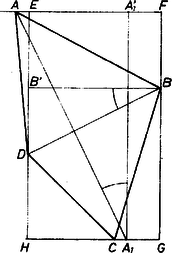

-vel.

2. ábra

Így

A_{1} A'_{1} ⊥ B B'

, ezért az

A A_{1} A'_{1}

és a

D B B'

derékszögű háromszögben az

A_{1}

-nél,

D

-nél levő szög egyenlő, e háromszögek hasonlók. Megfelelő oldalpárjaik aránya egyenlő:

\begin{matrix} A A_{1} : D B = A_{1} A'_{1} : B B', \\ A A_{1} = \frac{A_{1} A'_{1}}{B B'} \cdot D B = \frac{H E}{F E} \cdot D B = \frac{b}{m} \cdot D B, \end{matrix}

ahol

b

egy tetszőleges egyenlő oldalú háromszög alapjának a fele,

m

a magassága. (Felhasználtuk az I. megoldás megállapítását a keresett téglalap oldalairól.) Eszerint

A A_{1}

hosszát megadja egy

2 \cdot B D

alapú szabályos háromszög magassága, ezt felmérve

A

-ból a

B D

-re merőlegesen (

B D

-n túlra vagy közelítve hozzá), és a téglalap

C

-n átmenő oldala csak a

C A_{1}

egyenes lehet. A további oldalegyenesek ebből kiadódnak.
A szerkesztés helyességének bizonyításához csak a felhasznált háromszögre kell hivatkoznunk, másrészt ellenőriznünk kell, hogy az

A

B

C

D

csúcsok a téglalap oldalszakaszain legyenek. (A 2. ábrán az

A

kissé kiesik, ebben az esetben tehát nincs megoldása a feladatunknak.)
A szerkesztés végrehajtása azon múlik, hogy

A_{1}

-ként a

C

-től különböző pontot kapunk-e vagy nem. Ha

A_{1}

azonosnak adódik

C

-vel (a 2. ábrán olyan helyzetet mutatunk be, amelyen közel áll hozzá), akkor a rajta átmenő

G H

egyenes szabadon választható bizonyos korlátok között.
Megjegyzések. 1. Itt és az I. megoldásban lényegesen különbözőnek látszó feltételt kapunk a végrehajtás egyértelműségére. Megmutatjuk, hogy az előbbi feltétel azonos az utóbbival, vagyis ha az ottani teljesül ‐ ti.

Q

egybeesik

P

-vel ‐, akkor

A_{1}

is azonos

C

-vel (3. ábr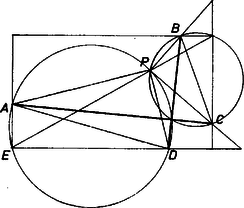a).

3. ábra

Ekkor az

A D P

és

C B Q

(azaz

C B P

) háromszögek egyező körüljárásúan hasonlók, így van olyan

P

centrumú forgatva nyújtás, mely az első háromszöget a másodikba viszi át, ennek szöge, az irányt is hozzáértve,

A P C ∢ = D P B ∢

. Ez pedig azt jelenti, hogy a

P

centrumú,

P C / P B = \sqrt[]{3}

arányú és (alkalmas irányban)

90^{\circ}

-os forgatva nyújtás

B D

-t

C A

-ba viszi át, tehát

A C ⊥ D B

és

A C = \sqrt[]{3} \cdot B D

. (Az olvasó gondolja át, hogy a második feltétel teljesüléséből is következik az elsőnek a teljesülése.)
2. Az

A A_{1}

szakasz szerkesztése egyszerűbb, ha

B D

-re mindkét partján szabályos háromszöget szerkesztünk, az új csúcsok távolsága

A A_{1}