Feladat: 1545. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: -
Füzet: 1975/április, 153 - 154. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Pont körüli forgatás, Húrnégyszögek, Gyakorlat
Hivatkozás(ok):Feladatok: 1974/október: 1545. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a feladatban szereplő kört k-val, a B-n átmenő, OB-re merőleges egyenest t-vel.

 

 

1. ábra
 

Az OB, AC egyenesek szimmetrikusak a t tengelyre, hiszen merőlegesek rá, így t-re szimmetrikus az OB-t B-ben érintő k kör is, és az AC szakasz is. Az ABC háromszög tehát egyenlő szárú, és az AC alapján levő BAC szög egyenlő az ugyancsak egyenlő szárú ABO háromszög ABO szögével, hiszen e két szög AB szára közös, és AC||OB. Mivel az AB egyenes elválasztja a C és O pontokat, az ABC, ABO háromszögek körüljárása ellentétes, amiből következik, hogy a BA-t CA-ba vivő forgatás iránya megegyezik az AB-t OB-be vivő forgatással. Tehát BAC és ABO mint forgásszögek is egyenlőek, és ugyanez igaz a CBA, BOA szögekre is. Forgassuk el B körül a CBO háromszöget, hogy C az A-ba kerüljön, O új helyzetét jelöljük E-vel. Ekkor a BOA, OBE forgásszögek is egyenlőek, tehát OB elválasztja az A és E csúcsokat. Emiatt az ABO, EOB háromszögek szimmetrikusak OB felezőpontjára, F-re nézve, és így AE felezi OB-t. Az előbb alkalmazott, BC-t BA-ba vivő B körüli forgatás CO-t AE-be viszi, e két utóbbi egyenes metszéspontja tehát rajta van az AC szakaszhoz és CBA látószöghöz tartozó látókörön, k-n. Ez a metszéspont tehát azonos k-nak és OC-nek a metszéspontjával, D-vel, tehát AD valóban felezi OB-t, amint azt bizonyítanunk kellett (1. ábra).
 

Megjegyzés. Megoldásunk utolsó lépésében felhasználtuk, hogy az AC szakaszhoz és a CBA forgásszöghöz mint látószöghöz tartozó mértani hely a k kör. Vagyis k a mértani helye azoknak a P pontoknak, amelyekre igaz az, hogy a PC egyenest ugyanakkora P körüli forgatás viszi a PA egyenesbe, mint amekkora B körüli forgatás BC-t BA-ba viszi. Nem kell az A, C pontokat sem kizárnunk a mértani hely pontjai közül, megállapodunk abban, hogy a PC egyenes a k C-beli érintőjét jelenti, ha P azonos C-vel, és hasonlóan PA az A-beli érintő, ha P azonos A-val. Ezen a ponton elkerülhettük volna a forgásszögekre való hivatkozást, ha arra hivatkozunk, hogy az OC egyenes biztosan metszi az AB szakaszt, így az AD és OC szakaszok biztosan metszik egymást és a metszéspont az ABO háromszögön belül van, így mindenesetre AC-nek ugyanazon az oldalán van a metszéspont, mint a B csúcs.
 

II. megoldás. Jelöljük AB és OC metszéspontját P-vel, és húzzunk P-n át OB-vel párhuzamos egyenest.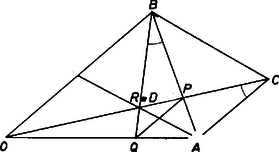
 

 

2. ábra
 

Messe ez OA-t Q-ban, ekkor az ACP és ABQ háromszögekben CAP∢=BAQ∢ (az I. megoldás alapján), és AC:AB=AB:OB=AP:AQ. Tehát az ACP és ABQ háromszögek hasonlóak, így ACP∢=ABQ∢. Jelöljük OC és BQ metszéspontját R-rel, akkor az AR szakasz a C és B pontokból egyenlő szögben látszik, és ezek a pontok az AR egyenesnek ugyanazon az oldalán vannak. Tehát ACBR húrnégyszög, vagyis R rajta van k-n, azaz R és D azonos. Az OBPQ trapéz átlóinak metszéspontja D, a szárak metszéspontja A, tehát AD felezi a párhuzamos oldalakat, így BO-t is (2. ábra).
 

III. megoldás. Jelöljük a BO egyenest O-ban érintő, A-n átmenő kört g-vel, k és g A-tól különböző metszéspontját M-mel (ezek a körök nem érinthetik egymást, hiszen k érinti OA-t és 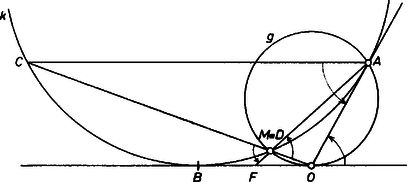g nem).
 

 

3. ábra
 

Az MO-t MA-ba vivő forgatás g O-beli érintőjét OA-ba viszi, OB||AC miatt ugyanakkora forgatás viszi AC-t OA-ba és MC-t MA-ba. Tehát az O, M, C pontok egy egyenesen vannak, vagyis M azonos D-vel. Jelöljük AD és OB metszéspontját F-fel. Erre a pontra FM⋅FA=FB2, és FM⋅FA=FO2, tehát F felezi az OB szakaszt (3. ábra).