Feladat: 1544. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: -
Füzet: 1975/szeptember, 15 - 19. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Szögfelező egyenes, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1974/október: 1544. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. A keresett háromszög AB, AC oldalegyenese szimmetrikus az adott f egyenesre, tehát P-nek f-re vonatkozó P* tükörképe rajta van az AC egyenesen. Ha P* nem azonos Q-val, a P*, Q pontok meghatározzák az AC egyenest, ennek f-fel alkotott metszéspontja a háromszög A csúcsa. A másik két csúcs megszerkesztése érdekében meghatározzuk a három szögfelező O metszéspontját (a háromszögbe írt kör középpontját).

 

Az O pont a PQ egyenes A-val ellentétes oldalán van. Az AOP szög az ACO háromszög külső szöge, tehát
AOP∢=α2+γ2.(1)
Hasonlóan kapjuk, hogy
AOQ∢=α2+β2.(2)
ahol α, β, γ a keresett háromszög szögei. Ezek alapján a keresett O pontból a PQ szakasz
POQ∢=AOP∢+AOQ∢=90∘+α2
szög alatt látszik. Mivel A helyzete és α értéke már ismert, ez a szög is megszerkeszthető, a megfelelő látókörív kimetszi f-ből O-t, és a PO, QO egyenesek pedig az AQ, AP egyenesekből rendre kimetszik a C, B csúcsokat.
 

2. A szerkesztés első lépése, A meghatározása végrehajtható, ha P* nem azonos Q-val, és P*Q nem párhuzamos f-fel. Az α=PAQ∢ nem lehet 180∘, tehát akkor sem folytathatjuk a szerkesztést, ha P*Q⊥f-re. Ha ez nincs így, akkor α alapján mindig megszerkeszthetjük az O pontot. A konkrét szerkesztés történhet például a következő lépésekben. Jelöljük PQ és f metszéspontját F-fel, tegyük be az APF háromszöget fordítva az AFP szögletbe, kapjuk az A'P'F háromszöget, hasonlóan AFQ fordítottja legyen A''FQ'. Húzzunk párhuzamost P-n át A'P'-vel, Q-n át A''Q'-vel, ezek metszéspontja legyen K. A K körüli, P-n átmenő k kör PQ-nak A-val ellentétes oldalán levő íve a keresett látókör‐ív. k és f O metszéspontjából továbbmenve azonban csak akkor kapunk háromszöget, ha a PO, QO félegyenes metszi rendre az AQ, AP félegyenest.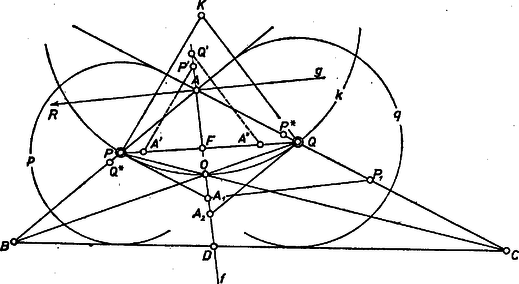
 

 

1. ábra
 

Ha a PP* félegyenest P körül úgy fordítjuk el, hogy a PP* egyenes A-t nem tartalmazó oldalára kerüljön, az elforgatásból kapott félegyenes egészen addig metszi az AP* félegyenest, amíg párhuzamos nem lesz vele. Jelöljük A-nak PP* felezőpontjára vonatkozó tükörképét A1-gyel. Az APA1P* négyszög rombusz, és a PO, AQ félegyenesek akkor és csakis akkor metszik egymást, ha O az AA1 szakaszon van. Legyen Q-nak f-re vonatkozó tükörképe Q*, A-nak QQ* felezőpontjára vonatkozó tükörképe pedig A2. A fentiekhez hasonlóan látható be, hogy a QO és AP félegyenesek akkor és csakis akkor metszik egymást, ha O az AA2 szakaszon van.
Vizsgáljuk meg először az AP≦AQ esetet, vagyis azt, amikor P közelebb van f-hez, mint Q. Ekkor AA1≦AA2, a hiányzó csúcsok szerkesztésének a feltétele tehát ebben az esetben az, hogy O az AA1 szakaszon legyen. Nézzük meg, rögzített A, P, f mellett hol vehetjük fel a Q-t, ha ennek a teljesülését biztosítani akarjuk.
Emeljünk A1-ben merőlegest f-re, messe ez AP*-ot P1-ben. PA1P1∢=PA1A∢+AA1P1∢=α2+90∘, ha tehát Q azonos P1-gyel, akkor O azonos A1-gyel. Ha Q a P*P1 szakasz belsejében van, akkor A1-ből a PQ szakasz α2+90∘-nál kisebb szög alatt látszik, tehát A1 kívül van k-n, és O az AA1-szakasz belsejében van. Ha viszont Q a P*P1 félegyenes P1 en túli pontja, akkor PA1Q∢>α2+90∘, tehát O az AA1 félegyenes A1-en túli pontja lesz. Jelöljük a P, Q pontoknak f-től mért távolságát p-vel, q-val. Könnyen látható, hogy Q akkor és csakis akkor van a P*P1 szakasz belsejében, ha q<2p. Ez tehát a szerkesztés végrehajtásának a feltétele, ha q≧p. Hasonlóan kapjuk, hogy p≧q mellett a megfelelő feltétel p<2q. Ha viszont p=q, akkor P*Q∥f, tehát az eddig mondottakat összefoglalva kapjuk, hogy a szerkesztés elvégzésének feltétele:
12<pq<2,p≠q,PQnem merőlegesf-re,  (3)
és természetesen f elválasztja a P, Q pontokat. Adott P, f mellett a megfelelő Q pontok mértani helyét a 2. ábra szemlélteti. (A vonalkázott síksáv pontjai felelnek meg, kivéve közülük a vastagon rajzolt szakasz és egyenesek pontjait.)
 

 

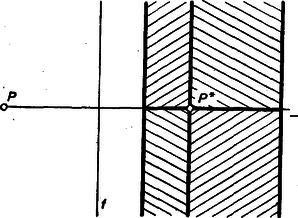2. ábra
 

3. Megmutatjuk, hogy ha a szerkesztés végrehajtható, akkor helyes eredményre vezet. Valóban, a kapott ABC háromszögben f szögfelező, mert AB, AC szimmetrikus rá. O-ból a BC szakasz ugyanakkora szög alatt látszik, mint a háromszögbe írható kör O1 középpontjából. Ez csak úgy lehet, ha O azonos O1 gyel, hiszen ha f és BC metszéspontját D-vel jelöljük, a DO1 szakasz pontjaiból a BC szakasz BO1C szögnél nagyobb szög alatt látszik, a DO1 félegyenes O1-en túli darabjának a pontjaiból pedig BC a BO1C szögnél kisebb szög alatt látszik.
 

4. Meg kell még vizsgálnunk, hogy valóban csak akkor létezik megoldás, ha a szerkesztés végrehajtható. Könnyen látható, hogy ez csak lényegében van így, ha ugyanis Q azonos P*-gal, akkor végtelen sok megoldás van, a szerkesztés mégsem hajtható végre a fentiek szerint. Ebben az esetben A az f egyenes tetszőleges, F-től különböző pontja lehet, és az A pont felvétele után a szerkesztés további lépései éppúgy végrehajthatók, mint a többi esetben. Ezzel a kiegészítéssel már pontosan igaz az állításunk, vagyis az, hogy ha az ABC háromszögben AB≠AC, akkor mindig teljesül (3). Ekkor ugyanis P* és Q különbözőek, és mivel mindkettő az AC egyenesen van, és ez sem nem párhuzamos f-fel, sem nem merőleges rá, már csak azt kell belátnunk, hogy 12<pq<2. Ez viszont ‐ mint láttuk - ekvivalens azzal, hogy a PO, AQ, valamint a QO, AP szakaszok metszik egymást, ami nyilván teljesül minden háromszögben.
 

II. megoldás (vázlat). Szerkesszük meg az A csúcsot ugyanúgy, mint az I. megoldásban. Mivel P egyenlő távolságra van a BC, AC egyenesektől, BC érinti a P középpontú, AC-t érintő p kört. Ugyancsak érinti BC a Q középpontú, AB-t érintő q kört. Ez a két kör szerkeszthető, a BC egyenes tehát a p, q körök közös érintőjeként megszerkeszthető.
 

Megjegyzések. 1. Jelöljük a háromszög A-beli külső szögfelezőjét g-vel, g és BC metszéspontját R-rel (tegyük most fel, hogy AB≠AC). Belátható, hogy R rajta van a PQ egyenesen, tehát A megszerkesztése után R is könnyen megkapható. Így viszont már ismerjük a BC egyenes egyik pontját, a II. megoldásban elég volna tehát a p, q körök egyikét megrajzolni, és ahhoz rajzolni R-ből érintőt.
2. Szimmetria és egyéb meggondolásaink a belső felező helyén külső szögfelezőre is érvényesek. Így bizonyos P, Q, f helyzetekben, amikor megállapításunk szerint "nincs megoldása'' a feladatnak, olyan ABC háromszög adódik, amelyben f az A-nál levő külső szögeket felezi, PO és QO egyike szintén külső szögfelező és O átveszi a háromszöghöz hozzáírt (azaz külső érintő) körök valamelyike középpontjának a szerepét.
3. Ha az olvasó összehasonlítja az I. megoldást a II. megoldással, vagy a saját megoldásával, csodálkozva kérdezheti, miért olyan hosszú az I. megoldás. Sokszor elmondtuk már, a teljes megoldáshoz ‐ szerkesztés esetében ‐ nem elég a szerkesztés lépéseit sorra elmondani, azt is meg kell vizsgálni, mindig végrehajtható-e a mondott szerkesztés, mindig helyes eredményre vezet-e, és ha igen, hány megoldást kapunk. Ezeket a részeket azonban mi magunk se vesszük mindig ilyen részletesen sorra, mint ezt az I. megoldásban tettük. Nem tehetjük, mert ‐ nincs rá helyünk. Ha már érezhetően sokat vagyunk kénytelenek elhagyni a teljes megoldásból, erre általában felhívjuk az olvasó figyelmét. De ez csak az egyik oka a megoldások változó hosszának. Nem mindig juthatunk vissza ugyanis a diszkusszióban ‐ a lehetséges esetek különválasztásában ‐ a kiindulási adatokig. Van, hogy csak annyit mondhatunk, hogy ha bizonyos metszéspont valahol a szerkesztési lépések elvégzése során létrejön, akkor van megoldás, vagy hogy annyi megoldás van, ahány metszéspontot kapunk. Az is előfordulhat, hogy az eredményt még külön ellenőrizni kell, és általában nem mondhatunk mást, mint hogy a szerkesztés helyes eredményre vezet ‐ ha a kapott eredményre teljesülnek bizonyos feltételek. Elmondhatjuk tehát, hogy a teljes megoldás részei csak pontatlanul körvonalazhatók. Mit javasolhatunk mégis a pontverseny résztvevőinek? Törekedjenek a teljességre. Ne elégedjenek meg a megoldás alapötletének megtalálásával. A dolgozat kiértékelésekor mi általában nem azt vizsgáljuk, elérnek-e azok bizonyos eleve adott színvonalat, hanem azt, kik jutottak legtovább a kérdés vizsgálatában.