Kezdőlap


Feladat:	1533. matematika gyakorlat	Korcsoport: 18-	Nehézségi fok: -
Füzet:	1976/október, 68 - 69. oldal		PDF \| MathML
Témakör(ök):	Kocka, Térfogat, Számtani-mértani egyenlőtlenségek, Szélsőérték-feladatok differenciálszámítás nélkül, Tetraéderek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1974/május: 1533. matematika gyakorlat

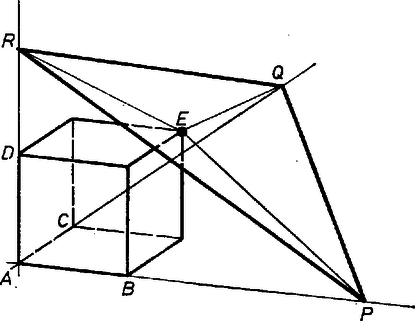
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszuk egységnek a kocka élét, és jelöljük az $A P, A Q, A R$ szakaszok hosszát rendre $p$ -vel, $q$ -val, $r$ -rel. Az $A P Q R$ tetraéder összeállítható az $A P Q E, A Q R E, A R P E$ tetraéderekből, amelyek mindegyikében az $E$ -hez tartozó magasság a kocka valamelyik oldaléle, tehát egységnyi.

A szemközti lapok területének kétszerese rendre

p q, q r, r p

, tehát az

A P Q R

tetraéder térfogatának hatszorosa

\begin{matrix} 6 V = p q + q r + r p . \end{matrix}

(1)

Mivel ebben a tetraéderben az

A P Q

alap területe

\frac{1}{2} p q

, és a hozzá tartozó magasság

r

, a térfogatot közvetlenül kiszámolva kapjuk, hogy

\begin{matrix} 6 V = p q r . \end{matrix}

(2)

Ezek szerint

\begin{matrix} p q + q r + r p = p q r, \end{matrix}

azaz

\begin{matrix} \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = 1. \end{matrix}

(3)

Ha a

P Q R

sík merőleges

A E

-re, az

A E

egyenes körül forgatva önmagába megy át. Mivel az

A E

egyenes körüli

120^{\circ}

-os forgatás a kockát önmagába viszi át, ez történik a

P Q R

háromszöggel is, tehát ebben az esetben

p = q = r

. Ez (3) szerint csak úgy lehetséges, ha

p = q = r = 3

, amikor is (2) szerint

V = 4, 5

térfogategység. Azt kell tehát belátnunk, hogy ha a pozitív

p, q, r

számokra teljesül (3), akkor

\begin{matrix} p q r \geq 27, \end{matrix}

(4)

és itt egyenlőség csak a

p = q = r = 3

esetben lehet.
Jelöljük a

\frac{3}{p}, \frac{3}{q}, \frac{3}{r}

számokat rendre

x, y, z

-vel.

Ezek is pozitívak, és velük megfogalmazva a bizonyítandó állítást, azt kapjuk, hogy ha

\begin{matrix} x + y + z = 3, \end{matrix}

(3a)

akkor

\begin{matrix} x y z \leq 1, \end{matrix}

(4a)

és itt egyenlőség csak akkor van, ha

x = y = z = 1

. Jelöljük

x + y

értékét

w

-vel, akkor

{(x - y)}^{2} \geq 0

miatt

4 x y \leq w^{2}

, tehát

\begin{matrix} 4 x y z \leq w^{2} z = w^{2} (3 - w) = 4 - {(w - 2)}^{2} (w + 1) . \end{matrix}

Itt

w > 0

miatt

{(w - 2)}^{2} (w + 1) \geq 0

, tehát valóban

4 x y z \leq 4

, és egyenlőség csak abban az esetben lehet, ha

w = 2

és

4 x y = w^{2}

, azaz

x = y = z = 1

. Állításunk bizonyítását ezzel befejeztük.