Kezdőlap


Feladat:	1532. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Fábián Csaba , Hujter Mihály
Füzet:	1975/december, 214 - 215. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Terület, felszín, Trapézok, Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1974/május: 1532. matematika gyakorlat

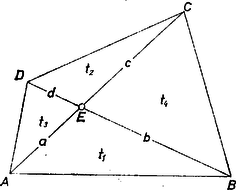
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

\begin{matrix} \sqrt[]{t} = \sqrt[]{t_{1}} + \sqrt[]{t_{2}} . \end{matrix}

(1)

Jelöljük az

A E

B E

C E

D E

szakaszok hosszát rendre

a

-val,

b

-vel,

c

-vel,

d

-vel, és az

A D E

B C E

háromszögek területét

t_{3}

-mal,

t_{4}

-gyel.

Mivel (1) mindkét oldalán pozitív mennyiség áll, (1) ekvivalens a belőle négyzetre emeléssel kapott

\begin{matrix} t = t_{1} + t_{2} + 2 \sqrt[]{t_{1} t_{2}} \end{matrix}

feltétellel, amiből

\begin{matrix} t = t_{1} + t_{2} + t_{3} + t_{4} \end{matrix}

(2)

alapján a

\begin{matrix} t_{3} + t_{4} = 2 \sqrt[]{t_{1} t_{2}} \end{matrix}

(3)

feltételt kapjuk.
Az

A B E

B C E

háromszögek

A E

C E

oldalának egyenese közös, ezért e háromszögek területének aránya:

\begin{matrix} t_{1} : t_{4} = a : c . \end{matrix}

(4)

Hasonlóan kapjuk,hogy

\begin{matrix} t_{3} : t_{2} = a : c, \end{matrix}

tehát

t_{1} : t_{4} = t_{3} : t_{2}

, azaz

t_{1} t_{2} = t_{3} t_{4}

, így (1) és (3) ekvivalensek a

\begin{matrix} t_{3} + t_{4} = 2 \sqrt[]{t_{3} t_{4}} \end{matrix}

feltétellel, amiből a

\begin{matrix} {(\sqrt[]{t_{3}} - \sqrt[]{t_{4}})}^{2} = 0 \end{matrix}

feltételt, és ebből az

\begin{matrix} t_{3} = t_{4} \end{matrix}

(5)

feltételt kapjuk. Azt fogjuk megmutatni, hogy (4) akkor és csakis akkor teljesül, ha

A B | | C D

.
A már bizonyított (4) összefüggéshez hasonlóan kapjuk, hogy

\begin{matrix} t_{1} : t_{3} = b : d, \end{matrix}

tehát

\begin{matrix} \frac{t_{3}}{t_{4}} = \frac{t_{1} t_{3}}{t_{1} t_{4}} = \frac{a d}{c b} . \end{matrix}

Emiatt (5) ekvivalens az

\begin{matrix} a : b = c : d \end{matrix}

(6)

feltétellel, ez pedig azzal, hogy az

A B E

C D E

háromszögek hasonlóak, vagyis

A B | | C D

, amint azt bizonyítani akartuk.

Fábián Csaba (Székesfehérvár, József A. Gimn.)

Hujter Mihály (Pápa, Türr I. Gimn.)

Megjegyzés. Azt, hogy a négyszög konvex, több helyen is felhasználtuk: ez biztosítja, hogy

E

belső pont, ami kell (2)-höz, és a legutolsó lépéshez, amelyben kihasználtuk, hogy az

A B E

C D E

háromszögek "egymással szemben'' vannak.