Kezdőlap


Feladat:	1531. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Zelhofer Walter
Füzet:	1976/október, 67 - 68. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Körülírt kör, Beírt kör, Hozzáírt körök, Hossz, kerület, Gyakorlat
Hivatkozás(ok):	Feladatok: 1974/május: 1531. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a $B$ -beli és a $C$ -beli érintők metszéspontja $D$ , és messe az $A$ -beli érintő az előbbi kettőt rendre $F$ -ben, $E$ -ben. A derékszög kizárása folytán e metszéspontok mindig létrejönnek, hiszen az $A B C$ háromszögnek egyik oldala sem átmérő a körülírt $k$ körben, és így az érintők közt nincsenek párhuzamosak. Az érintő szakaszok egyenlők : $D B = D C, E C = E A, F A = F B$ .

1. ábra

D E F

háromszög oldalait az érintőszakaszokból kizárólag összeadással kapjuk, ha az

A B C

háromszög hegyesszögű (1. ábra), illetve vegyesen összeadással és kivonással, ha az

A B C

háromszögben tompaszög is van (a 2. ábrán az

A

csúcsná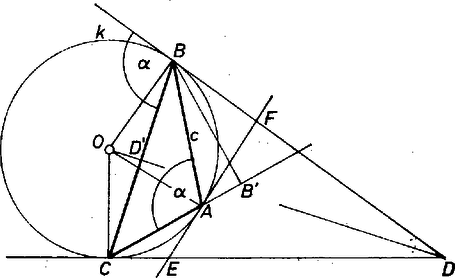l).

2. ábra

Más szóval: az adja ezt a megkülönböztetést, hogy

k

D E F

háromszögnek az 1. ábrán beírt köre, a 2. ábra felvételében pedig az

E F

oldalához hozzáírt, külső érintő köre. Mindkét esetben

E F = E A + A F

, az 1. ábrán hasonlóan

F D = F B + B D

és

D E = D C + C E

, viszont a 2. ábrán

F D = B D - B F, D E = C D - C E

. Így a

D E F

háromszög

p

kerülete az 1. és a 2. ábra esetében rendre

\begin{matrix} p_{1} = 2 (B D + C E + A F), p_{2} = 2 \cdot B D . \end{matrix}

D B

érintőszakasz hosszát a

D B D'

derékszögű háromszögből számítjuk, ahol

D'

D

-nek

B C

-n levő vetülete, vagyis a

B C

oldal felezőpontja. A

D' B D

szög érintőszárú kerületi szög a

k

-ban, pontosabban az a

B C

ív van a szárai között, amely rendre nem tartalmazza, illetve tartalmazza az

A

csúcsot. Így az 1. ábra esetében

D' B D ∢ = α

, a 2. ábrán

D' B D ∢ = 180^{\circ} - α

. Rendre ugyanekkora a

B' A B

szög, ahol

B'

B

csúcs vetülete az

A C

egyenesen (az

A C

szakaszon, illetve ennek

A

-n túli meghosszabbításán), így a

B D D'

és

A B B'

háromszögekből, a szokásos rövid jelölésekkel mindkét esetben

\begin{matrix} B D = \frac{B D'}{A B'} \cdot A B = \frac{a c}{2 \cdot A B'} . \end{matrix}

A B'

vetület hosszát úgy kapjuk, hogy Pitagorasz tételét alkalmazzuk a

B B' C

és

B B' A

háromszögek közös befogójára. A két helyzet szerint

C B' = C A \mp A B' = b \mp A B'

, így

\begin{matrix} B' B^{2} = B C^{2} - B' C^{2} & = B A^{2} - B' A^{2}, \\ a^{2} - {(b \mp A B')}^{2} & = c^{2} - B' A^{2}, \\ A B' & = \frac{b^{2} + c^{2} - a^{2}}{\pm 2 b} . \end{matrix}

Eszerint a hegyesszögű, illetve a tompaszögű háromszög esetében

\begin{matrix} B D = \frac{a b c}{c^{2} + b^{2} - a^{2}}, ill. B D = \frac{a b c}{a^{2} - b^{2} - c^{2}} . \end{matrix}

Az elsőből az

A, B, C

, az

a, b, c

, valamint a

D, E, F

betűket ciklikusan fölcserélve

\begin{matrix} C E = \frac{b c a}{a^{2} + c^{2} - b^{2}}, A F = \frac{c a b}{b^{2} + a^{2} - c^{2}}, \end{matrix}

és így a kerület keresett kifejezései:

\begin{matrix} p_{1} = 2 a b c (\frac{1}{c^{2} + b^{2} - a^{2}} + \frac{1}{a^{2} + c^{2} - b^{2}} + \frac{1}{b^{2} + a^{2} - c^{2}}), p_{2} = \frac{2 a b c}{a^{2} - b^{2} - c^{2}} . \end{matrix}

Az előforduló nevezők mindegyike pozitív, ugyanis bármelyiknek az eltűnéséből Pitagorasz tételének megfordítása alapján az következnék, hogy az

A B C

háromszög valamelyik szöge derékszög.

Zelhofer Walter (Mosonmagyaróvár, Kossuth L. Gimn.)

Megjegyzés.

A B'

kifejezését gépiessé tette volna a cosinustétel alkalmazása. De ez sem tette volna mellőzhetővé a 2. ábra esetének külön vizsgálatát.