Feladat: 1526. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: -
Füzet: 1974/november, 145 - 146. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Egyéb sokszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1974/április: 1526. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszuk egységnek az ötszög oldalát, és jelöljük a legnagyobb szög nagyságát ω-val, a legkisebbét ϱ-val. A feladat feltevése szerint ω<120∘, és azt kell belátnunk, hogy ϱ>90∘. Mivel az ötszög szögeinek az összege nem kisebb (4ω+ϱ)-nál, ez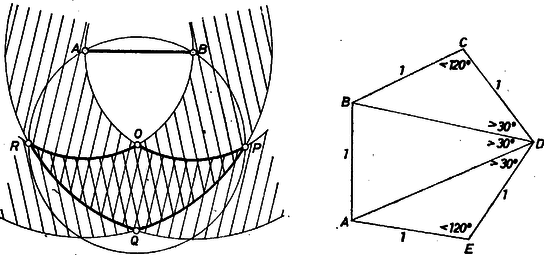ért

4ω+ϱ≥540∘,
amiből ω-120∘ alapján ϱ>60∘ következik. Eszerint az ötszög szögei 60∘ és 120∘ közöttiek, tehát az átlók nagysága 1 és 3 között van. (Az 1 szárakkal szerkesztett egyenlő szárú háromszögben ‐ amilyet alkot egy szabályos háromszög két csúcsa és a középpontja ‐ az alap hossza 3.) Tekintsük az ötszög egyik oldalát, és írjunk a végpontjai körül 1 és 3 sugarakkal köröket. A választott oldallal szemközti csúcsnak a körök által határolt körgyűrűkben kell lennie: megmutatjuk, hogy emiatt ebből a csúcsból a szemközti oldal 30∘-nál nagyobb szög alatt látszik.
 

 

Jelöljük a választott oldal végpontjait A-val, B-vel, az egységnyi sugarú körök egyik metszéspontját O-val, és a két körgyűrű közös részének O-val megegyező oldalon levő darabkájának a további csúcsait P-vel, Q-val, R-rel. Ekkor (mint az könnyen igazolható) ABO, BOP, AOR szabályos háromszögek, és OQ<1. Tehát a körívekkel határolt OPQR idom belseje benne van az O körüli egység sugarú körben. Ennek a körnek a belső pontjaiból az AB szakasz az AB^-hez tartozó kerületi szögnél nagyobb szög alatt látszik, s mivel ez a kerületi szög az O-t tartalmazó oldalon 30∘-os, állításunkat beláttuk.
Beláttuk tehát, hogy az AB-vel szemközti D csúcsra ADB∢>30∘. A BCD háromszög egyenlő szárú, és benne BCD∢<120∘. Emiatt BDC∢>30∘, és hasonlóan ADE∢>30∘. Tehát az ötszög D-nél levő szögére
CDE∢=BDC∢+ADB∢+ADE∢>90∘
teljesül: ez a szög tompaszög. Mivel az ötszög tetszőleges oldalából indultunk ki, ezzel beláttuk, hogy az ötszög mindegyik szöge tompaszög.