Feladat: 1518. matematika gyakorlat Korcsoport: 18- Nehézségi fok: -
Füzet: 1975/február, 67 - 70. oldal  PDF  |  MathML 
Témakör(ök): Nim, Konstruktív megoldási módszer, Prímtényezős felbontás, Gyakorlat
Hivatkozás(ok):Feladatok: 1974/március: 1518. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1000 prímtényezős alakban 23⋅53. Így a feladathoz adott útmutatás szerint osztóinak száma (3+1)(3+1)=16.

 

Ezek az osztók:
 


1, 2, 4, 8, 5, 10, 20, 40, 25, 50, 100, 200, 125, 250, 500, 1000.
 


Ezek osztóinak száma:
 


1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16.
 


Az osztókat a számok prímtényezős alakjából állapíthatjuk meg.
 

Először a feladat második felére válaszolunk. A játékot az veszti el, aki az 1000-et kimondja. 1000-nek 16 osztója van, 16-nál kevesebb osztója csak két számnak van, 500-nak és 200-nak, mindkettőnek 12 osztója. A kezdő játékosnak nem érdemes sem 200-at, sem 500-at mondani, mert akkor ellenfele a másik számot mondja, a kezdőnek csak az 1000 jut, és így veszít. A következő legtöbb osztóval rendelkező szám a 100, ennek 9 osztója van. Láthatjuk, hogy ha a kezdő játékos éppen a 100-at mondja, akkor ellenfele csak a 200, 500 és 1000 számok között válogathat. Akármelyiket is választja, biztosan veszít: ha 1000-et mondja, akkor a szabályok szerint vesztett. Ha viszont 200 és 500 valamelyikét mondta, akkor a kezdő a másikat mondja, a második játékosnak csak az 1000 marad, veszített. Így a módosított játék esetén a kezdő játékosnak a 100-at kell mondania, és biztosan megnyeri a játékot.
A feladat első felére nehezebb válaszolni, mert az egyes számok közötti további oszthatósági viszonyok nehézzé teszik a probléma átlátását. Ahhoz, hogy jobban lássuk, melyik szám melyiknek osztója, helyezzük el az 1000 osztóit a következő alakban, ahogyan azt az 1. táblázatban láthatjuk:
 


|1000500250125|2001005025|4020105|8421|1. táblázat
 |1000500250125|200|40|8|2. táblázat

 

Figyeljük meg, ha a táblázatból kiválasztunk egy számot, akkor osztói vagy ugyanabban az oszlopban alatta, vagy a jobbra eső oszlopban és ugyanabban a sorban, vagy a lejjebb fekvő sorban helyezkednek el. Mondjuk azt, hogy egy szám "elfedi'' a táblázaton mindazokat a számokat, amelyek osztják. Így például a 20 a 20, 10, 5, 4, 2, 1 számokat fedi le, azt a jobb alsó sarkot, aminek 20 a csúcsa. A táblázatra átfogalmazva a játékot, az a következőképpen alakul: a két játékos felváltva a táblázat mezői közül választ azzal a feltétellel, hogy olyan mezőt nem választhatnak, amelyet egy korábban választott mező lefed. (Például az általuk választott mezővel együtt az összes olyan mezőt áthúzzák, melyeket az lefed, ilyenkor a következő játékosnak mindig az át nem húzott mezők közül kell válogatnia.) Az veszít, aki végül az 1000 feliratú mezőt, azaz a bal felső mezőt kénytelen választani.
Ahhoz, hagy a kezdő játékos nyerjen ‐ a táblázatot megfigyelve láthatjuk ‐, az kell, hogy kezdéskor a 100-at mondja. Ekkor a további játék számára csak a 2. táblázaton látható rész marad. Ha most a második játékos valamelyik számot mondja, akkor a kezdő mindig mondhatja annak szimmetrikus párját, hiszen az sem lesz lefedett. Így mindenképpen a második játékos kénytelen kimondani azt az egyetlen számot, aminek nincs szimmetrikus párja, vagyis az 1000-et. Ezzel megmutattuk, hogy a kezdő játékos 100-at mondva, biztosan nyeri a játszmát.
 

II. megoldás. Tekintsük az 1., illetve 2. ábrát.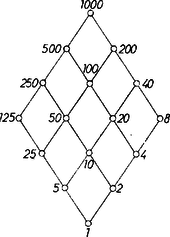
 

 

1. ábra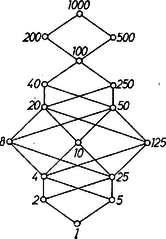
 

 

 

2. ábra
 

Azt mondjuk, hogy az ábra a csomópontja "kisebb'' az ábra egy b csomópontjánál, ha a következő két feltétel teljesül:
 

1. az a csomópont lejjebb van rajzolva a b csomópontnál.
2. a b csomópontból az ábrába berajzolt utak mentén csak lefelé haladva el tudunk jutni az a csomópontba.
Mind a két ábrában a legalsó csomópont "kisebb'' az összes többinél, a legfelső pedig "nagyobb'' az összes többinél.
Könnyen ellenőrizhető (ellenőrizzük !), hogy a feladatban szereplő két játék a következővel ekvivalens: Ketten felváltva választanak egy‐egy csomópontot az 1., ill. 2. ábrából, azzal a feltétellel, hogy olyan csomópontot nem választhatnak, ami egy korábban mondott csomópontnál "kisebb''. Az veszít, aki a legfelső csomópontot kénytelen választani. A két ábrán a csomópontok mellé írt számok a feladatban szereplő játékokkal való kapcsolat ellenőrzését könnyítik meg.
A továbbiakban tekintsünk egy tetszőleges olyan hálózatot, amelyben a legalsó csomópont "kisebb'' az összes csomópontnál, és az összes csomópont "kisebb'' a legfelső csomópontnál. Ilyet mutat a 3. ábra.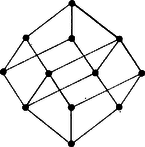
 

 

3. ábra
 

Megmutatjuk, hogy ha két játékos egy ilyen hálózaton játssza az előbb megfogalmazott játékot, úgy ha a kezdő ügyesen játszik, biztosan nyer.
 

Tekintsünk el ugyanis a legalsó ponttól. Ha a kezdő valamely más pontot mondva kezdi meg a játékot, a második játékos nem tudja a legalsó pontot mondani, az foglalt, ugyanis a feltétel miatt kisebb minden más pontnál. Ha van olyan, a legalsótól különböző csomópont, amivel a kezdő játékos kezdve, és ügyesen játszva (azaz az ellenfél minden lépésére megfelelőt lépve) nyerni tud, akkor a kezdő játékos ezzel kezdi a játékot, és nyer. Ha ilyen csomópont nincs az azt jelenti, hogy a kezdő játékos akármelyik, a legalsótól különböző csomópontot is mondja, az ellenfél meg tudja nyerni a játszmát, azaz ha az ellenfél "ügyesen'' játszik, nyer. Ha most el tudnánk érni, hogy a játékosok helyet cseréljenek, úgy ismét a kezdő játékos nyerne. De pontosan erre jó a legalsó csomópont! Hiszen ha a kezdő játékos ezt mondja, ellenfele kénytelen valamely más, a legalsótól különböző csomópontot mondani. Innen tovább a kezdő játékos pontosan úgy játszhat, mint ahogyan az ellenfele játszott volna.
A feladatban szereplő két játék "ábrája'' kielégíti a mondott feltételt, így valóban a kezdő játékos, "ha ügyesen játszik'', nyerni fog.
 

Megjegyzések. 1. A II. megoldásban csak azt bizonyítottuk be, hogy a kezdő játékos megfelelő módon játszva, biztosan nyerni fog. Viszont nem mondtuk meg, hogyan is kell játszania. A bizonyítás egzisztencia‐bizonyítás volt: létezik olyan "stratégia'', tud az első játékos úgy játszani, hogy nyerjen. A bizonyítás nem volt konstruktív: nem mondta meg azokat a szabályokat, amelyek szerint az első játékosnak játszania kell ahhoz, hogy nyerjen.
Ezzel szemben az első megoldásunk konstruktív volt: azon felül, hogy megmutattuk: nemcsak hogy az első játékos valóban meg tud nyerni minden játszmát, azt is megmondtuk, hogyan kell játszania. (Nemcsak a kezdő lépést adtuk meg, hanem azt is megmondtuk, hogy az ellenfél valamilyen lépésére melyik más lépéssel kell válaszolnia.)
 

2. Az első megoldás gondolatmenete a feladat első részére minden nehézség nélkül átvihető pkgk alakú számokra, ahol p és q különböző prímek, k>1 természetes szám. Ilyenkor a kezdő játékosnak pk-1qk-1-gyel kell kezdenie a játszmát, az ellenfél további lépéseire a szimmetrikus párját kell mondani. Ilyen szimmetrikus párok a pkqs és psqk, 0≤s≤k-1.
 

3. Amennyiben a feladatban 1000 helyett tetszőleges n-et mondunk, és elkészítjük a feladathoz tartozó hálózatokat, ugyanúgy, ahogyan azt a II. megoldásban tettük, akkor az így kapott hálózatok is kielégítik a II. megoldásban megfogalmazott feltételt. Így a feladatban leírt játékokat 1000 helyett tetszőleges n-nel elmondva, továbbra is igaz, hogy a kezdő, ha ügyesen játszik, mindig nyer. Azonban most meg tudtunk adni stratégiát is: hogyan játsszon a kezdő ahhoz, hogy nyerjen. Általában ez eddig még nem sikerült: csak azt tudjuk, tud ügyesen játszani, hogy hogyan, azt még nem. (Hasonló problémával foglalkozik Varga Tamás: Osztójátékok c. cikke. Lásd "Élő Matamatika I.'' 161‐178. old.)
 

4. A II. megoldásban leírt hálózatban definiálhatjuk két pont minimumát, valamint maximumát. Két pont minimuma az a pont, amelyik kisebb mind a kettőnél, és amire igaz az, hogy ha valamely pont kisebb a megadott két pontnál, akkor kisebb a két pont minimumánál. Hasonlóan definiálható két pont maximuma is. Egy hálózatban nem feltétlenül szükséges, hogy bármely két pontnak legyen minimuma és maximuma. Ha viszont ez teljesül, a hálózatot hálónak nevezzük. Az 1., 2. és 3. ábrán látható hálózatok egyúttal hálók is. A hálók igen fontos szerepet töltenek be a matematika legkülönbözőbb ágaiban, a halmazelméletben, logikában, valószínűségszámításban, gépi matematikában, a matematikai fizikában. Egy hálóban két pont, a és b minimumát a∩b -vel, maximumát a∪b -vel jelölik. Ha egy hálóban tetszőleges a, b, c elemekre
a∩(b∪c)=(a∩b)∪(a∩c)
igaz, akkor a hálót disztributív hálónak nevezik, (mert a disztributív tulajdonság is teljesül). Az ábrákon látható hálók egyike sem disztributív. Ha egy disztributív hálóban van legkisebb pont, amit 0-val, legnagyobb pont, amit 1-gyel jelölünk, valamint minden a ponthoz van a' pont, amire a ∩a'=0 és a ∪a'=1, akkor a hálót Boole‐algebrának nevezzük, George Boole (1815‐1864) angol matematikus után, aki először vizsgálta az ilyen struktúrákat. A Boole‐algebrák szoros kapcsolatban vannak gondolkodásunk leírásával.