| Feladat: | 1515. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: - |
| Füzet: | 1975/január, 18 - 19. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Körülírt kör, Diszkusszió, Háromszögek szerkesztése, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1974/február: 1515. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük az adott kört -val, középpontját -val, sugarát -rel, a magasságpontot -mel, az adott hosszúságú oldal végpontjait -val, -vel, a harmadik csúcsot -vel, -beli átellenes pontját -gyel, felezőpontját -fel. Ha az -n átmenő magasságvonalat tükrözzük -re, a tükörkép átmegy -n, és merőleges -re, tehát Thalész-tétele szerint -en is átmegy. Ugyancsak átmegy -en a -n átmenő magasságvonal -re vonatkozó tükörképe, tehát -nek -re vonatkozó tükörképe . Emiatt rajta van -nak az centrumú, arányú kicsinyítésből származó képén, -en. E kör középpontja az szakasz felezőpontja, sugara . 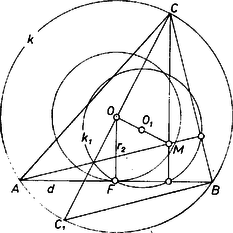 Pitagorasz-tétele szerint A kört megkapjuk, ha -ban tetszőleges hosszúságú húrt veszünk fel, ennek a húrnak -tól mért távolsága. Megszerkeszthetjük -et is, és metszéspontjainak egyike lesz . Mivel a két metszéspont szimmetrikus -re, az egyikből kapott háromszöget -re tükrözve a másikhoz tartozó megoldást kapjuk. Legyen tehát a metszéspontok egyike (vagy ha a két kör érinti egymást, legyen az érintési pont). -nek -re vonatkozó tükörképe , -nek -beli átellenes pontja , az , csúcsokat pedig az -re -ben emelt merőleges metszi ki -ból. Az így megszerkesztett háromszögnek körülírt köre, hossza , és a háromszög magasságpontja, hiszen az egyik csúcs átellenes pontjának a szemközti oldalfelezőpontjára vonatkozó tükörképe. A , körök létrejönnek, ha . E két kör metszi egymást, ha Ha tehát , nincs megoldás, esetén csak akkor van megoldás, ha rajta van -n, ekkor viszont végtelen sok megoldás van. Ha , a megoldások száma rendre , , vagy , ha hossza az , értékek közé esik, ezek egyikével egyenlő, vagy e határokon kívül esik. |