| Feladat: | 1514. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: - |
| Füzet: | 1979/január, 13 - 14. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kombinatorikus geometria síkban, Körök, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1974/február: 1514. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Tegyük fel, hogy három kört már lerajzoltunk, és ezek részre osztották a síkot. Tekintsünk egy tetszőleges negyedik kört és tegyük fel, hogy ennek darab közös pontja van az előzőekkel.  A negyedik kör legfeljebb pontban metszi az előző hármat, három kör pedig legfeljebb részre osztja a síkot, így négy kör legfeljebb részt hozhat létre. Ez el is érhető, amint azt a 2. ábra mutatja. 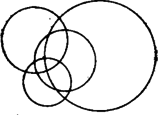 |