Feladat: 1502. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1977/szeptember, 14 - 16. oldal  PDF  |  MathML 
Témakör(ök): Beírt alakzatok, Egyenlő szárú háromszögek geometriája, Terület, felszín, Gyakorlat
Hivatkozás(ok):Feladatok: 1973/december: 1502. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Azt állítjuk, hogy a maximális területű kivágott szabályos 12-szög lemeznek az adott ABC=H háromszöglemez mindegyik oldalán van csúcspontja. Ha ugyanis egy S1 szabályos 12-szög teljesen a H belsejében van, akkor nagyítható az O1 középpontjábóI mint centrumból olyan S2-vé, amelynek legalább egy csúcsa (azaz O1-től legtávolabbi pontjainak egyike) rajta van H kerületén, de S2-nek nincs pontja H-n kívül. Legyen egy ilyen csúcsa D2 és H-nak ehhez támaszkodó oldala AB. Ha S2-nek nincs pontja az AC, BC oldalak egyikén sem, akkor nagyítható az előbbi korlátozás mellett S3-má úgy a D2 centrumból, hogy S3-nak már van egy E3 csúcsa, mondjuk AC-n. És ha S3 teljesen az A-t tartalmazó felében volna a BC-vel kettévágott síknak, akkor az A centrumból való alkalmas arányú nagyítással előálló S4 szabályos 12-szögnek már a lemez BC oldalán is lesz egy F csúcsa; legyenek a D2-ből és E3-ból most nyert csúcsok 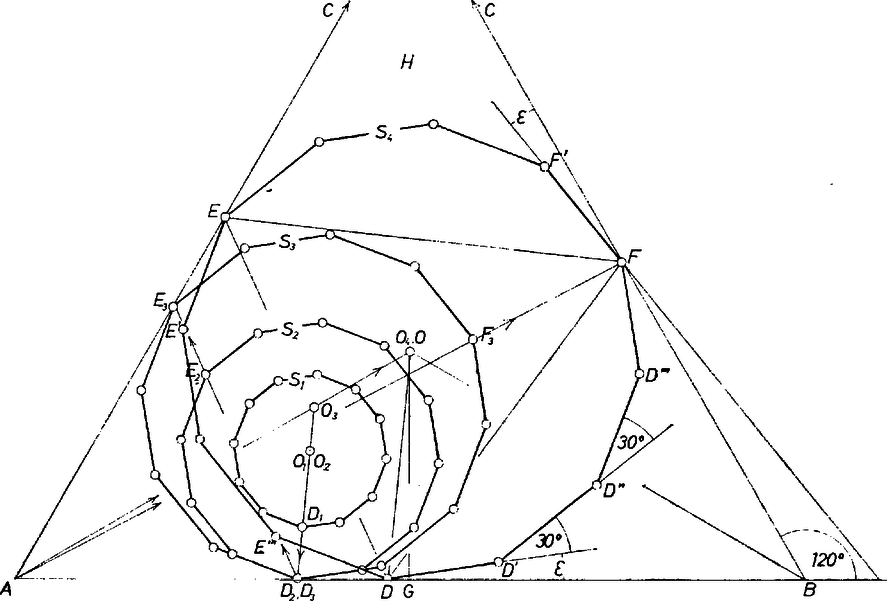D, ill. E.

 

 

Tegyük fel egyenlőre, hogy S4-nek D-ből induló oldalai közül egyik sem illeszkedik AB-re, ekkor tekintsük D-ből F felé haladva S4 egymás utáni oldalainak irányszögét AB-hez mint alapirányhoz viszonyítva. Azt akarjuk ezzel belátni, hogy F az S4-nek D-től számítva negyedik csúcsa. Mivel a szabályos 12-szög külső szöge 360∘/12=30∘, ezért az első (DD') oldal irányszöge 0∘ és 30∘ között van, a másodiké (D'D''-é) 30∘-kal nagyobb, tehát 30∘ és 60∘ között, a k-adiké (k-1)⋅30∘ és k⋅30∘ között. Másrészt BC irányszöge 120∘=4⋅30∘ vagyis a D-től számított 4. és 5. oldal irányszöge közé esik, és ez igazolja állításunkat. (Az 5. az FF'.) oldal egyenese már B-n túl metszi AB-t.) Hasonlóan az E csúcs sorszáma F-től is, D-től is 4, ennélfogva a DF, FE, ED átlók egyenlők.
Pontosabban megnézve az is adódik, hogy az F utáni FF' oldalnak BC-hez viszonyított ε irányszöge egyenlő a D'DB szöggel, így FDB∢=FDD'∢+ε=EFF'∢+ε=EFC∢=DEA∢, tehát a DFB,FEC,EDA háromszögek (egyező körüljárással) egybevágók, egymásba átvihetők a DFE háromszög O4 középpontja körüli 120°-os elfordításokkal. Ámde A-nak, B-nek és C-nek ciklikusan egymásba 120°-os elfordításokkal való átvitele csak H-nak O centruma körül lehetséges, eszerint S4-nek O4 középpontja azonos O-val.
Azt is föltehetjük, hogy a D'DB∢=E'''DA∢ ‐ ez csak jelölés dolga ‐, így DB≥DA.
Most már szinte nyilvánvaló, hogy az S4-nél nagyobb szabályos 12-szög lemez is kivágható H-ból. Ilyet így kapunk: S4-et addig fordítjuk el O körül, hogy DD' párhuzamos legyen AB-vel ‐ eközben D és az egész S4 a H belsejébe jut ‐, majd ezt a helyzetét nagyítjuk O-ból. Az arányt növelve D és D' (F, F' E, E') új helyzete egyszerre jut a háromszög kerületére és ennél nagyobb 12-szög nem vágható ki, hiszen akkor beírt körének sugara egyenlő a H-ba írt kör sugarával.
Mindjárt a nagyítások után adódott volna ez a helyzet, ha S1-nek egy oldala párhuzamos AB-vel, így DD' vagy DE''' ráesik AB-re.
 

2. A kapott helyzetben ODB szög fele akkora, mint a 12-szög belső szöge, eszerint BOD egyenlő szárú háromszög, D-t a B körüli BO sugarú körrel metszhetjük ki, így pedig DD'=2(DB-GB)=2⋅OB-AB=43CG-AB=(233-1)AB= 30,9 mm (ahol G az AB oldal felezőpontja).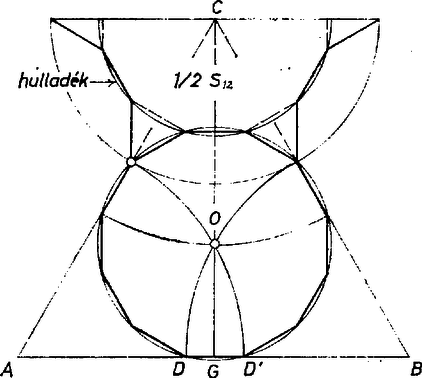
 

 

3. Ismeretes, hogy a szabályos 12-szög területe 3-szor akkora, mint a körülírt kör sugara fölé szerkesztett négyzet területe: 3⋅OD2.
3⋅OD2=3(OG2+DG2)=(2-3)AB2. A háromszöglemez területe (3/4)⋅AB2, a hulladék (53-8)/4⋅AB2, ez 5-83=0,381 része az adott lemez területének.