Kezdőlap


Feladat:	1496. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1974/szeptember, 17 - 18. oldal		PDF \| MathML
Témakör(ök):	Alakzatok szimmetriái, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Beírt kör, Hossz, kerület, Paralelogrammák, Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/november: 1496. matematika gyakorlat

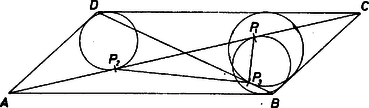
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a paralelogramma átlóinak metszéspontját $O$ -val, és legyenek a beírt köröknek az érintési pontjai rendre $P_{1}$ , $P_{2}$ , $P_{3}$ és legyen $A B \geq B C$ .
Először belátjuk, hogy $P_{1} O = O P_{3}$ .

A kör tengelyes szimmetriájából következik, hogy egy külső pontból a körhöz húzott érintőszakaszok hossza egyenlő. Ennek ismeretében könnyen igazolhatjuk a következő tételt: egy háromszög beírt körének az oldallal való érintési pontja úgy osztja az oldalt, hogy a csúcstól az érintési pontig terjedő szakasz a fél kerület és a csúccsal szemközti oldal különbségével egyenlő.^{$^{*}$}
Alkalmazzuk az előbbi tételt az

A B C

és

B C D

háromszögre és fejezzük ki segítségükkel az

O P_{1}

O P_{3}

távolságokat.

\begin{matrix} O P_{1} = \frac{C A}{2} - C P_{1} = \frac{C A}{2} - (\frac{A B + B C + C A}{2} - A B) = \frac{A B - B C}{2}, \\ O P_{3} = \frac{D B}{2} - B P_{3} = \frac{D B}{2} - (\frac{B C + C D + D B}{2} - C D) = \frac{C D - B C}{2} . \end{matrix}

Mivel

A B C D

paralelogramma, így

A B = C D

, s ezzel állításunkat bizonyítottuk.
Másodszorra azt látjuk be, hogy

O P_{2} = O P_{1}

. Ez következik abból, hogy a paralelogramma középpontosan szimmetrikus, s középpontja az átlóinak metszéspontja.
A

P_{1}

P_{2}

P_{3}

pontok feltétel szerint egy egyenlő szárú derékszögű háromszög csúcsai. Az előbb bizonyított egyenlőségek miatt

P_{1} P_{3} = P_{2} P_{3}

lehet csak, azaz a derékszög a

P_{3}

csúcsban van, vagyis

P_{3} O

P_{1} P_{2}

felező merőlegese. Ez más szóval azt jelenti, hogy a paralelogramma átlói merőlegesek egymásra, tehát rombusz, és így

O P_{1} = O P_{2} = O P_{3} = 0

. Az érintési, pontok nem alkotnak háromszöget.
Nincs tehát egyetlen olyan paralelogramma sem, amely az adott feltételeknek eleget tenne.

^{$^{*}$}Lásd Horvay K. ‐ Reiman I.: Geometriai feladatok gyűjteménye. I. kötet, 44. oldal, 642. feladat.