Feladat: 1495. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: -
Füzet: 1974/október, 69 - 70. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Négyszögek geometriája, Szélsőérték-feladatok differenciálszámítás nélkül, Diszkusszió, Gyakorlat
Hivatkozás(ok):Feladatok: 1973/november: 1495. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az állítást először arra az esetre igazoljuk, ha a négyszögnek van párhuzamos oldalpórja.

 

 

1. ábra
 

Legyen AD||BC és AD≦BC, akkor BC oldal tartalmazza (A1-et, AD=BC esetén A1≡C), és AFFA1=1, ami ≦1.
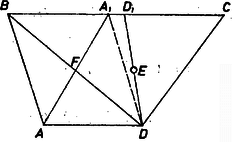
Ha nincs a négyszögnek párhuzamos oldalpária (2. ábra), akkor AB és CD oldalegyénesek metszéspontját jelöljük N-mel, AD és BC oldalegyénesek metszéspontját M-nel, - és válasszuk a betűzést úgy, hogy NA<NB és MA<MD legyen.
 

 

2. ábra
 

M és N metszéspontok mindegyike valóban létrejön és a négyszög csúcsai közül az A csúcs van legközelebb az MN egyeneshez. Tükrözzük az A csúcsot az F pontra, s jelöljük a képét A'-vel, ekkor DA'||AB és A' az AA1 egyenesen van. Elegendő azt belátnunk, hegy A' a négyszög belsejében van, ami teljesül, ha DA' félegyenes az ADC és BA' félegyenes az ABC (konvex) szögtartomány belsejében halad, ami igaz, mert AD és BC oldalak maghosszabbításai az AB egyenesnek a négyszöget nem tartalmazó partján metszik egymást, és ugyanígy az AB és CD egyenesek meghosszabbítása is.
Az AFFA'=1 és FA1>FA miatt AFFA'=1, s ezzel az állítást igazoltuk.
 

Megjegyzés. A megoldók közül többen felismerték, hogy az 1429*. gyakorlatból a feladat állítása rögtön következik. Ez ugyanis azt mondja ki, hogy ha egy konvex négyszög mindegyik csúcsát tükrözzük a vele szomszédos átló felezőpontjára, akkor az így kapott négy pont közül van olyan, amelyik a négyszög belsejében vagy kerületén van.
*Megoldása megjelent a 46. kötet 69‐70. oldal