Kezdőlap


Feladat:	1490. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1974/szeptember, 15 - 17. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Körülírt kör, Hossz, kerület, Síkgeometriai számítások trigonometria nélkül háromszögekben, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/október: 1490. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Állítsunk merőlegest az $A B$ oldalra a végpontjaiban és jelöljük az $A$ -ban emelt merőlegesnek a körrel való metszéspontját $B_{1}$ -gyel, a $B$ -ből kapott metszéspontot pedig $A_{1}$ -gyel (1. ábra).

1. ábra

Így a (félkörnél kisebb)

A B_{1}

és

B A_{1}

ívek pontjainak ‐ és csakis ezeknek ‐ az

A B

egyenesen levő vetületei esnek az

A B

szakasz egyik vagy másik meghosszabbítására. Thalész-tétele alapján

A A_{1}

és

B B_{1}

a körnek átmérői és ezért

A B_{1} = B A_{1}

.
Ugyanezt elvégezve a

B C

és a

C A

oldal esetében is, metszéspontként a

C

-ből induló átmérő

C_{1}

végpontját, valamint ismét

B_{1}

-et,

A_{1}

-et kapjuk, és a

B C

egyenesen a félkörnél kisebb, egymással egyenlő

B C_{1}

és

C B_{1}

ívek, a

C A

-n pedig a

C A_{1} = A C_{1}

ívek pontjai adnak a meghosszabbításra eső vetületet. Jelöljük a kapott

{\hat{A B}}_{1}

{\hat{B C}}_{1}

{\hat{C A}}_{1}

körívhez tartozó kerületi szöget rendre

γ_{1}

-gyel,

α_{1}

-gyel,

β_{1}

-gyel; ezekkel és a kör sugarával kifejezhetjük egyrészt a kérdéses ívösszegeket:

\begin{matrix} {\hat{A B}}_{1} + {\hat{B A}}_{1} = 2 \frac{2 π r 2 γ_{1}}{360^{\circ}} = \frac{π r}{45^{\circ}} γ_{1}, & (1) \\ {\hat{B C}}_{1} + {\hat{C B}}_{1} = \frac{π r}{45^{\circ}} α_{1}, {\hat{C A}}_{1} + {\hat{A C}}_{1} = \frac{π r}{45^{\circ}} β_{1}, \end{matrix}

másrészt az

A B C

háromszög szögeit.
Ha az eredeti

A B C

háromszög hegyesszögű (1. ábra), akkor az

A_{1}

B_{1}

C_{1}

pont a körből rendre a

B C

C A

A B

oldal által lemetszett (félkörnél kisebb) íven van és az (1)-ben felsorolt hat ív hézagtalanul és átfedés nélkül kitölti a kör kerületét. Ezért egyrészt

\begin{matrix} \frac{π r}{45^{\circ}} (α_{1} + β_{1} + γ_{1}) = 2 π r, α_{1} + β_{1} + γ_{1} = 90^{\circ}, \end{matrix}

továbbá arányukra a közlés szerint

\begin{matrix} γ_{1} : α_{1} : β_{1} = 1 : 2 : 3, \end{matrix}

amiből

γ_{1} = 15^{\circ}

α_{1} = 30^{\circ}

β_{1} = 45^{\circ}

, ezekből pedig háromszögünk szögei:

\begin{matrix} B A C ∢ & = β_{1} + γ_{1} = 60^{\circ}, C B A ∢ = γ_{1} + α_{1} = 45^{\circ}, \\ A C B ∢ & = α_{1} + β_{1} = 75^{\circ} . \end{matrix}

2. Tekintsük most a kérdéses ívösszegeket egy tompaszögű

K L M

háromszögben, legyenek ennek szögei rendre

κ

λ

μ

, úgy, hogy

μ > 90^{\circ} > λ \geq κ

, és állapítsuk meg a (fentiekhez hasonlóan vett)

{\hat{K L}}_{1} + {\hat{L K}}_{1}

{\hat{L M}}_{1} + {\hat{M L}}_{1}

és

{\hat{M K}}_{1} + {\hat{K M}}_{1}

összegek nagyságviszonyát, hogy a

K

L

M

csúcsokat helyesen feleltethessük meg a kívánt

A

B

C

csúcsoknak (2. ábra).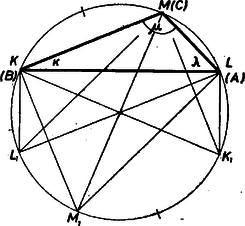

2. ábra

M

csúcsot nem tartalmazó

\hat{K L}

ív nagyobb félkörnél, ezen pontjainak sorrendje

K

L_{1}

M_{1}

K_{1}

L

, és az egymás utáni pontok közti ívek már mind kisebbek félkörnél.
Az ívek arányához elég lesz kifejeznünk a

{\hat{K L}}_{1}

, az

\hat{L_{1} M}

és a

{\hat{K M}}_{1}

ívekre néző kerületi szögeket:

\begin{matrix} K M L_{1} ∢ & = K M L ∢ - L_{1} M L ∢ = μ - 90^{\circ}, \\ L_{1} L M ∢ & = L_{1} L K ∢ + K L M ∢ = L_{1} M K ∢ + λ = (μ - 90^{\circ}) + λ = 90^{\circ} - κ, \\ K M M_{1} ∢ & = 90^{\circ} - K M_{1} M ∢ = 90^{\circ} - K L M ∢ = 90^{\circ} - λ . \end{matrix}

Mivel

κ \leq λ

, azért

L_{1} L M ∢ \geq K M M_{1} ∢

, továbbá a

K M L_{1}

szög mindkettőjüknél kisebb, mert

{\hat{K L}}_{1}

\hat{L_{1} M}

-nek is, a

{\hat{K M}}_{1}

-nek is része. És mivel az

1 : 2 : 3

arány tagjai különbözők, azért

\begin{matrix} {\hat{K L}}_{1} : {\hat{K M}}_{1} : {\hat{M L}}_{1} = 1 : 2 : 3, \end{matrix}

és a

K L

oldal szerepét

A B

-nek,

K M

-ét

B C

-nek és

M L

szerepét

C A

-nak kell átadnunk, azaz

K

L

M

szerepét rendre

B

-nek,

A

-nak,

C

-nek. Az arányokból egyrészt

\begin{matrix} 2 {\hat{K L}}_{1} = {\hat{K M}}_{1} = {\hat{K L}}_{1} + {\hat{L_{1} M}}_{1} = {\hat{K L}}_{1} + \hat{L M}, \\ {\hat{K L}}_{1} = \hat{L M}, μ - 90^{\circ} = κ; \end{matrix}

másrészt

\begin{matrix} 3 {\hat{K L}}_{1} = {\hat{M L}}_{1}, \hat{M K} = 2 \hat{M L}, λ = 2 κ, \end{matrix}

Ezeket behelyettesítve

\begin{matrix} κ + λ + μ = κ + 2 κ + (90^{\circ} + κ) = 180^{\circ}, \\ κ = A B C ∢ = 22, 5^{\circ}, λ = B A C ∢ = 45^{\circ}, μ = A C B ∢ = 112, 5^{\circ} \end{matrix}

3. Mindezek szerint a partnerünk által alapul vett

A B C

háromszög egymás utáni szögei vagy

60^{\circ}

45^{\circ}

75^{\circ}

, vagy

45^{\circ}

22, 5^{\circ}

112, 5^{\circ}

. ‐ Mondhatjuk ezt is: az

A

B

C

csúcs vagy egy szabályos

12

-szögnek rendre az első, a hatodik, ill. a tizedik csúcsával azonos, vagy pedig egy szabályos

8

-szögnek rendre az első, a hatodik, a nyolcadik csúcsával.

Megjegyzés. Derékszögű nem lehetett az

A B C

háromszög, mert akkor az átfogó egyenesén nem lenne a hosszabbításra eső vetületi pont, a megfelelő ív arányszám

0

lenne az adottaktól eltérően.