Feladat:	1487. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Telek József
Füzet:	1974/szeptember, 13 - 15. oldal		PDF  |  MathML
Témakör(ök):	Egyenletek grafikus megoldása, Egyenletek, Egyenlőtlenségek grafikus megoldása, Elsőfokú (és arra visszavezethető) egyenlőtlenségek, Egészrész, törtrész függvények, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/október: 1487. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle \left[\frac{2x-1}{3}\right]+\left[\frac{4x+1}{6}\right]=\frac{5x-4}{3}\mathrm{.}}\end{array}$ (1) I. megoldás. A megoldáshoz felhasználjuk a következő összefüggést: $\left[a\right]=a-\left\{a\right\}$, ahol $\left\{a\right\}$ az $a$ törtrészét jelenti, azaz $0\le \left\{a\right\}<1$. Eszerint (1) így alakul: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{2x-1}{3}-\left\{\frac{2x-1}{3}\right\}+\frac{4x+1}{6}-\left\{\frac{4x+1}{6}\right\}=\frac{5x-4}{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle \left\{\frac{2x-1}{3}\right\}+\left\{\frac{4x+1}{6}\right\}=\frac{7-2x}{6}\mathrm{.}}\hfill & \text{(<mn>2</mn>)}\end{array}}$ Mivel $0\le \left\{a\right\}<1$, a (2) bal oldalán álló összeg $0$ és $2$ közé esik, így $\begin{array}{c}{\displaystyle 0\le \frac{7-2x}{6}<2}\end{array}$ is fennáll, ebből $\begin{array}{c}{\displaystyle -2\mathrm{,}5<x\le 3\mathrm{,}5.}\end{array}$ A kapott $x$ értéket (1) jobb oldalába helyettesítve: $\begin{array}{c}{\displaystyle -5\mathrm{,}5<\frac{5x-4}{3}<4\mathrm{,}5.}\end{array}$ (3) Mivel az (1) bal oldalán álló kifejezések mindegyike egész, ezért összegük is egész, azaz $\frac{5x-4}{3}=N$ egész. (3)-ból $N$ értéke $-5\mathrm{,}5$ és $4\mathrm{,}5$ közé eső érték lehet. Írjuk fel táblázatban $N$ szóba jövő értékeit, számítsuk ki a hozzájuk tartozó $x=\frac{3N+4}{5}$ értékeket, helyettesítsük ezeket az (1) bal oldalán álló kifejezésekbe. Összegüket egybevetve $N$-nel [ami (1) jobb oldalának megfelelő értéke] mindjárt kiolvashatjuk a táblázatból, hogy mikor áll fenn egyenlőség.   ${\displaystyle \begin{array}{ccccccccccc}{\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>N</mi></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>5</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>4</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>3</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>4</mn></math>}}\hfill \\ {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2</mn><mn>,</mn><mn>2</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn><mn>,</mn><mn>6</mn></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0</mn><mn>,</mn><mn>4</mn></math> }}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>2</mn></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>8</mn></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn><mn>,</mn><mn>4</mn></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mn>,</mn><mn>6</mn></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mn>,</mn><mn>2</mn></math>}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">[</mo><mrow><mrow><mfrac><mrow><mn>2</mn><mi>x</mi><mo stretchy="false">-</mo><mn>1</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow><mo fence="true" stretchy="true">]</mo></mrow></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn></math>}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">[</mo><mrow><mrow><mfrac><mrow><mn>4</mn><mi>x</mi><mo stretchy="false">+</mo><mn>1</mn></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></mrow><mo fence="true" stretchy="true">]</mo></mrow></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn></math> }}\hfill \end{array}}$   Tehát az egyenlőség $x=-0\mathrm{,}4$; $0\mathrm{,}2$; $0\mathrm{,}8$; $1\mathrm{,}4$; $2\mathrm{,}0$; értékekre teljesül.    Telek József (Budapest, Berzsenyi D. Gimn. II. o. t.)   II. megoldás. Ábrázoljuk a 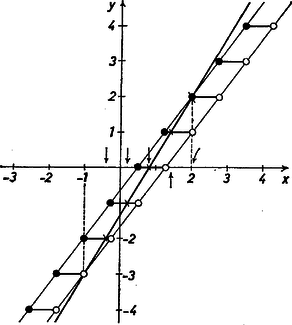$\left[\frac{2x-1}{3}\right]+\left[\frac{4x+1}{6}\right]$ és az $\frac{5x-4}{3}$ függvényeket.     Az egészrész függvény grafikonja az $x$ tengellyel párhuzamos szakaszokból áll. Mindig egész $y$ értéket vesz fel. A szakasz jobb oldali végpontja hozzátartozik a függvényhez, a bal oldali nem. A grafikonról leolvashatjuk, hogy a két függvénynek közös pontja van az $y=2$, $y=1$, $y=0$, $y=-1$, $y=-2$ függvények egy-egy szakaszán. A hozzájuk tartozó $x$ értékeket pontosan meghatározhatjuk. Ha $\frac{5x-4}{3}=2$, akkor $x=2$, és így tovább $x$-re a következő értékeket kapjuk: $x=2$, $\frac{7}{5}$; $\frac{4}{5}$; $\frac{1}{5}$; $-\frac{2}{5}$.   Megjegyzés. Hasonló típusú egyenletek megoldásánál a grafikonról leolvashatjuk, hogy a megoldások száma attól függ, hányszor metszi át az adott egyenes az egészrész függvényt ábrázoló szakaszokat. A szakaszok végpontjai két párhuzamos egyenesen helyezkednek el. Nincs megoldás, ha az egyenletben megadott egyenes mindenütt a két párhuzamos közti sávon kívül halad. Végtelen sok megoldás van, ha az egyenes a sávon belül halad, nem párhuzamos az $x$ tengellyel, vagy egybeesik valamelyik szakasszal.   III. Megoldás. Tekintsük új ismeretlennek az első szögletes zárójelben álló kifejezést: $\begin{array}{c}{\displaystyle y=\frac{2x-1}{3}\mathrm{,}}\end{array}$ (4) erre az ismeretlenre (1) a $\begin{array}{c}{\displaystyle \left[y\right]+\left[y+\frac{1}{2}\right]=\frac{5y-1}{2}}\end{array}$ (5) egyenletet jelenti. A bal oldalon álló szám $n\le y<n+\frac{1}{2}$ mellett (ahol $n$ egész szám) $2n$-nel, $n+\frac{1}{2}\le y<\left(n+1\right)$ mellett $\left(2n+1\right)$-gyel egyenlő. Mindkét esetben egyenlő a bal oldal $\left[2y\right]$-vel, (5) tehát ekvivalens a $\begin{array}{c}{\displaystyle \left[2y\right]=\frac{5y-1}{2}}\end{array}$ (6) egyenlettel. Ebből némi átalakítással a $\begin{array}{c}{\displaystyle 2y-\left[2y\right]=\frac{1-y}{2}}\end{array}$ egyenletet kapjuk. Itt a bal oldal értéke $0$ és $1$ közötti szám ($0$ lehet, de $1$ nem), tehát a jobb oldalon álló kifejezés értéke is ilyen: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 0\le \frac{1-y}{2}<\mathrm{1,}}\hfill \\ \hfill {\displaystyle -1<y\le 1.}\hfill \end{array}}$ Eszerint (6) bal oldalának lehetséges értékei: $\left[2y\right]=-2$, $-1$, $0$, $1$, $2$, amiből (6), majd (4) alapján rendre ${\displaystyle \begin{array}{ccccccccc}\hfill {\displaystyle y}& {\displaystyle =-\frac{3}{5};}\hfill & {\displaystyle -\frac{1}{5};}\hfill & \hfill {\displaystyle }& {\displaystyle \frac{1}{5};}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle \frac{3}{5};}& {\displaystyle }\hfill & {\displaystyle \mathrm{1,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =-\frac{2}{5};}\hfill & {\displaystyle \frac{1}{5};}\hfill & \hfill {\displaystyle }& {\displaystyle \frac{4}{5};}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle \frac{7}{5};}& {\displaystyle }\hfill & {\displaystyle 2}\hfill \end{array}}$ adódik. Behelyettesítéssel ellenőrizhetjük, hogy ezek mindegyike gyöke (1)-nek.