Feladat: 1483. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: -
Füzet: 1974/április, 162 - 164. oldal  PDF  |  MathML 
Témakör(ök): Elsőfokú (és arra visszavezethető) egyenletrendszerek, Kombinatorikai leszámolási problémák, Lineáris programozás, Nomogramok, Maradékos osztás, Szöveges feladatok, Gyakorlat
Hivatkozás(ok):Feladatok: 1973/szeptember: 1483. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A háromszög egymás utáni szögei a feltételeknek megfelelően egy‐egy x, y, z természetes számnak rendre a 7-szerese, 9-szerese, 11-szerese úgy, hogy

7x+9y+11z=180.(1)

Mivel e szögek mindegyike hegyesszög, kisebb 90∘-nál, teljesülnek a következő egyenlőtlenségek:
1≦x≦12,1≦y≦9,1≦z≦8.(2)
Átrendezve (1)-et:
9(x+y+z)=180+2(x-z).(3)

Ennek az egyenletnek a bal oldala osztható 9-cel, ezért a jobb oldalon (x-z) is osztható vele, ami csak akkor teljesül a (2) feltételek miatt, ha x-z=0, vagy ha x-z=9. Ezt a két lehetőséget külön vizsgáljuk.
 

a) Ha x-z=0, akkor z=x, és így (2) miatt x≦8, másrészt (3)-ból és ismét (2) miatt
y=20-2x≦9,x≧6.
Így a következő három lehetőség adódik:
x=z=6,7,8,y=8,6,4,
a megfelelő szögértékek:
7x=56,49,42,9y=36,54,72,11z=88,77,66.
Innen tehát 3 megoldást kaptunk.
 

b) Ha pedig x-z=9, akkor z=x-9, a (3), majd (2) alapján 2x+y=31 és x≧11, az ennek megfelelő értékhármasok:
x=12,11z=x-9=13,12,és  ekkor  y=17,19,
és a lehetséges szögértékek:
7x=84,ill.779y=63,ill.81 és11z=33,ill.22.
Mindezek szerint a feltételnek 5 háromszög tesz eleget, s ezek szögei:
α=42∘,49∘,56∘,77∘,84∘,β=72∘,54∘,36∘,81∘,63∘,γ=66∘,77∘,88∘,22∘,33∘,

Megjegyzések. Bemutatjuk a feladatnak egyféle grafikus próbálkozáson alapuló megoldását. Felhasználjuk az egyenlő oldalú háromszögnek azt a tulajdonságát, hogy bármely belső vagy kerületi pontjára nézve a három oldaltól mért távolságok összege állandó, egyenlő a háromszög magasságával (l. ábra, bizonyítását az olvasóra hagyjuk).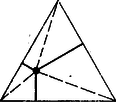
 

 

1. ábra
 

Ennek megfordításával ugyanis minden olyan x, y, z nemnegatív számokból álló számhármashoz, melyben x+y+z=s, állandó, az s magasságú egyenlő oldalú háromszögben egyértelműen hozzárendelhető egy pont, pontosabban akkor, ha még azt is előírjuk, hogy az x, y, z távolságot a háromszögnek rendre melyik oldalától mérjük.
A gyakorlat céljára ennek alapján úgynevezett "számoló'' (számítást pótló) ábrát lehet szerkeszteni úgy, hogy a háromszögben már előre mindegyik oldalegyenestől 1, 2, ..., (vagy 10, 20, ...) egységnyi távolságban párhuzamosakat húzunk. Ezután ‐ föltéve, hogy ismerjük x és y értékét ‐ megkeressük azt a pontot, ahol az első oldaltól x, és a második oldaltól y távolságban húzott egyenes metszi egymást, és leolvassuk a harmadik oldallal párhuzamos egyenesek skálaértékei alapján a pontnak a harmadik oldaltól való távolságát, ez az adott x-et és y-t s-re kiegészítő z érték. x-et és y-t a grafikonba bevinni, illetőleg z-t onnan kiolvasni, bizonyos pontossággal lehet az ábra nagyságának és a hálózat sűrűségének megfelelően, mint bármely grafikonban. A 2. ábrán s=180∘ és a megjelölt pontban az α=110∘, β=20∘ értékpárhoz γ=50∘ adódik. ‐ Az ilyen ábrákat háromszög nomogramnak nevezik. A skálákat a háromszög oldalaira is lehet fölírni.
 

 

2. ábra
 

Rátérve feladatunkra, mivel háromszögünk szögei hegyesszögek, elég megtartani a 2. ábrából a középháromszöget (hullámosan körülkerítve), és ennek magasságát 90 egységnek, foknak megfeleltetni. Az így szerkesztett 3. ábrán az egyik oldallal párhuzamosan csak azokat az egyeneseket húzzuk meg, amelyek a csonkítatlan háromszög oldalegyeneseitől akkora távolságban vannak, mint az új háromszög magasságának 790, 1490, ..., 8490 része, a másik oldaltól 990, 1890, ..., 8190 része és a harmadiktól 1190, 2290, ..., 8890 része.
 

 

3. ábra
 

Továbbá megkeressük az olyan pontokat ‐ ha vannak ‐, amelyeken 3 berajzolt egyenes megy át, és kellő ellenőrzés után ezek a feladat megoldásai.
Az érdeklődő olvasónak figyelmébe ajánljuk az így talált 5 pont (és a kerületen levő, derékszögű háromszöget jelentő pont) kölcsönös helyzetében mutatkozó szabályszerűség kimondását, valamint felhasználását a három oszthatósági feltételt kielégítő tompaszögű megoldások kiolvasására.