Kezdőlap


Feladat:	1473. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1974/március, 111 - 112. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Vetítések, Indirekt bizonyítási mód, Térgeometriai bizonyítások, Tetraéderek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/április: 1473. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tegyük fel a feladat állításával ellentétben, hogy van olyan tetraéder, amelyben minden csúcsnál van derékszög.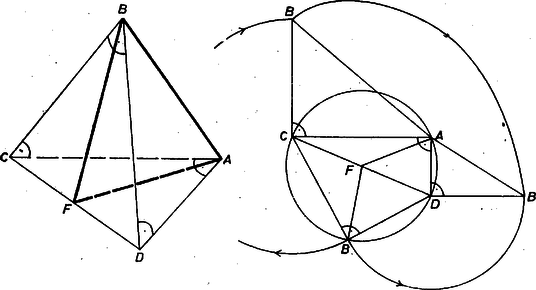
Legyen $A B C D$ egy ilyen tetraéder, és válasszuk a betűzést úgy, hogy $A B$ legyen az (egyik) leghosszabb él. E választás miatt az $A B C$ , $A B D$ háromszögekben $A B$ -vel szemben van a legnagyobb szög, tehát a $C$ -nél levő élszögek közül az $A B C$ háromszögbeli szög a derékszög, a $D$ -nél levők közül pedig az $A B D$ -beli. (Minden háromszögben csak egy derékszög lehet.) Így ezeknek a háromszögeknek $A$ -nál hegyesszögük van, az $A$ -nál levő derékszög csak az $A C D$ háromszögben lehet. Ugyanígy kapjuk, hogy a $B$ -nél levő derékszög a $B C D$ háromszögnek szöge.

1. ábra

Jelöljük a

C D

szakasz felezőpontját

F

-fel. Thalész tétele szerint az

A F

B F

szakaszok egyenlők a

C D

átfogó felével. Mivel az

A B

C D

egyeneseknek nincs közös pontjuk, az

A

B

F

pontok valódi háromszöget határoznak meg, és ebben

\begin{matrix} A B < A F + F B = \frac{1}{2} C D + \frac{1}{2} C D = C D \end{matrix}

(az 1. ábra a gondolt gúlát és kiterítését vázolja). Ellentmondásra jutottunk, hiszen betűzésünk szerint a tetraédernek nincs

A B

-nél hosszabb éle. ‐ Feladatunk állítását ezzel bebizonyítottuk.

II. megoldás.
Tegyük ismét fel, hogy

A B C D

olyan tetraéder, amelyben minden lap derékszögű és minden csúcsnál van derékszög. Egyelőre csak a

C

-ben összefutó élek közti szögeket tekintjük, válasszuk úgy a betűzést, hogy

C

-ben az

A C B

szög legyen

90^{\circ}

-os. Mivel minden lap derékszögű háromszög, a tetraéder lapjain nincsenek tompaszögek. Emiatt a

C

-nél levő

A C D

és

B C D

szögek hegyesszögek, a

D

csúcs a

C

-ben

C A

-ra emelt merőleges

S_{A}

síknak

A

-t tartalmazó oldalán, és a

C

-ben a

C B

-re emelt merőleges

S_{B}

síknak

B

-t tartalmazó oldalán van. Ezek szerint

D

-nek az

A B C

síkon levő

D_{0}

a vetülete benne van

A C B

szögtartományban.
Vetítsük

D_{0}

-t az

A C

B C

egyenesekre és jelöljük a vetületet rendre

D_{1}

-gyel,

D_{2}

-vel. A

D_{0} D_{1} C D_{2}

négyszögben három

90^{\circ}

-os szög van, ez tehát téglalap (2. ábra).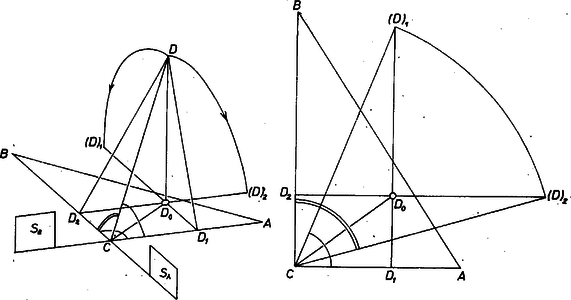

2. ábra

C D_{1} D_{0}

és

C D_{1} D

háromszögek derékszögűek, bennük

C D_{1}

közös és

D D_{1} > D_{0} D_{1}

. Emiatt

D C D_{1} ∢ > D_{0} C D_{1} ∢

. Hasonlóan kapjuk, hogy

D C D_{2} ∢ > D_{0} C D_{2} ∢

, és e kettő összege szerint

A C D ∢ + B C D ∢ = D_{1} C D ∢ + D_{2} C D ∢ > D_{1} C D_{0} ∢ + D_{2} C D_{0} ∢ = 90^{\circ}

, tehát a

C

-nél levő hegyesszögek összege nagyobb

90^{\circ}

-nál.
Amit

C

-re kaptunk, érvényes a tetraéder további három csúcsára is, a bennük találkozó hegyesszögek összege is több

90^{\circ}

-nál. Így viszont a négy lapon levő

8

hegyesszög összege

360^{\circ}

-nál több volna, ami nem lehet, hiszen egy-egy lapon az összegük

90^{\circ}

.
A kívánt tetraéder tehát nem létezik.