Kezdőlap


Feladat:	1471. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1974/április, 157 - 159. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Magasságvonal, Körülírt kör, Feuerbach-kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/április: 1471. matematika gyakorlat

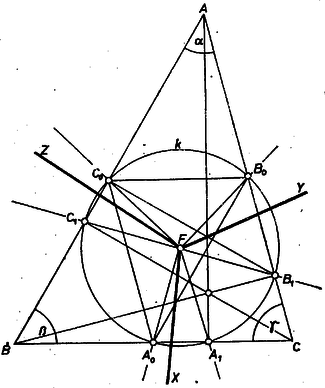
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük az $A_{0} B_{0} C_{0}$ háromszög köré írt $k$ kört. Azt állítjuk hogy az $A_{1}$ , $B_{1}$ , $C_{1}$ pontok mindegyike rajta van $k$ -n. A magasságtalppontok egyenrangú szerepéből következik, hogy elegendő az állítást egyik pont esetében igazolni. Legyen ez a pont $B_{1}$ .

A_{0} B_{0} C_{0}

háromszög oldalai az

A B C

háromszög középvonalai, így a két háromszög hasonló és a szokásos jelölés szerint

C_{0} A_{0} B_{0} ∢ = C A B ∢ = α

A_{0} B_{0} C_{0} ∢ = β

B_{0} C_{0} A_{0} ∢ = γ

, továbbá

A_{0} B_{0} = \frac{1}{2}

A B = C_{0} A

. Az

A B B_{1}

derékszögű háromszögben

C_{0} A = C_{0} B_{1}

, (az átfogó Thalész‐körének sugara), és így

A_{0} B_{0} = C_{0} B_{1}

is fennáll. Mivel még

B_{0} B_{1}

párhuzamos

A_{0} C_{0}

-lal, azért az

A_{0} B_{0} B_{1} C_{0}

négyszög szimmetrikus trapéz, azaz írható köréje kör, és ennek középpontja

F

; állításunkat bebizonyítottuk.
Nem használtuk fel a

B_{0}

B_{1}

pontoknak olyan tulajdonságát, amely megkülönböztetné őket az

A_{0}

A_{1}

és

C_{0}

C_{1}

pontpártól, sem feladatunk szögadatait, ezért az

A_{0} B_{0} C_{0}

háromszög köré írt körön minden háromszögben rajta van az

A_{1}

C_{1}

magasságtalppont is. Ezt a kört a háromszög Feuerbach‐féle körének^{$^{*}$} nevezik.
A most szerzett ismereteink felhasználásával számítsuk ki a

B_{1} F B_{0}

szöget.
Az ugyanazon íven nyugvó kerületi és középponti szögek között fennálló ismert összefüggés alapján

\begin{matrix} A_{0} F B_{0} ∢ = 2 A_{0} C_{0} B_{0} ∢ = 2 γ, \\ A_{0} F B_{1} ∢ = 2 A_{0} B_{0} B_{1} ∢ = 2 α, \end{matrix}

amiből

\begin{matrix} B_{1} F B_{0} ∢ = | A_{0} F B_{0} ∢ - A_{0} F B_{1} ∢ | = 2 | γ - α_{0} | \end{matrix}

adódik minden háromszögre.
A fenti

C_{0} B_{1}

ill.

A_{0} B_{0}

szakasz a trapéz átlója vagy oldala lesz aszerint, hogy a

B_{1}

pont az

A C

oldal felezőpontjához viszonyítva melyik csúcshoz van közelebb. A

B_{1}

pont helyzetét az

α

és

γ

szögek közt fennálló nagyságviszony szabja meg. Ha

α < γ

, akkor

90^{\circ} - α > 90^{\circ} - γ

, és mivel nagyobb szöggel szemben nagyobb oldal van,

B_{1}

C

csúcshoz közelebb kerül, mint az

A

-hoz.
A feladat szögadatai szerint a

α < β < γ

, így a másik két esetben is felírhatjuk ezt a különbséget:

\begin{matrix} A_{1} F A_{0} ∢ = 2 (γ - β), C_{1} F C_{0} ∢ = 2 (β - α) . \end{matrix}

Most már könnyen felírhatjuk a feladatban szereplő

F X

F Y

F Z

félegyenesek közti szögeket. Tekintsük pl. az

X F Y

szöget. Mivel

γ > α

és

γ > β

, azért az

A_{1}

és

B_{1}

magasságtalppontok mindegyike közelebb van a

C

csúcshoz, mint az

A_{0}

B_{0}

oldalfelezőpont. Így

\begin{matrix} X F Y ∢ & = A_{0} F B_{0} ∢ - (A_{0} F X ∢ + B_{0} F Y ∢) = 2 γ - {\frac{1}{3} 2 (γ - α) + \frac{1}{3} 2 (γ - β)} = \\ = \frac{2}{3} (α + β + γ) = 120^{\circ} . \end{matrix}

Hasonló, de mégsem egészen ez a helyzet az

Y F Z

szög esetében. Most, mivel

α < β

és

α < γ

, a

B_{0}

C_{0}

felezési pontok közelebb vannak az

A

csúcshoz, mint

B_{1}, C_{1}

és így

\begin{matrix} Y F Z ∢ & = B_{0} F C_{0} ∢ + \frac{1}{3} B_{1} F B_{0} ∢ + \frac{1}{3} C_{0} F C_{1} ∢ = 2 α + \frac{1}{3} {2 (γ - α) + 2 (β - α)} = \\ = \frac{2}{3} (α + β + γ) = 120^{\circ} . \end{matrix}

E két eredmény alapján

Z F X ∢ = 120^{\circ}

is teljesül.
Végeredményben a kérdezett félegyenesek által bezárt szögek nem függnek a háromszög szögeitől. A szögek számértéke csak azt a célt szolgálta, hogy a versenyzők el tudják dönteni az oldalfelező és magasságtalppontok sorrendjét az egyes háromszögoldalakon.

^{$^{*}$}Ez a kör az

M

magasságpontból felére kicsinyített képe a háromszög köré írt körnek, ezért felezi a magasságvonalaknak a magasságpont és a csúcs közé eső szakaszát is. Erre tekintettel használják rá a "9 pont köre'' elnevezést is, néhol pedig "Euler‐köre'' néven említik. Könnyű látni a tett kiegészítés alapján, hogy az

M A B

M B C

M C A

háromszögek Feuerbach‐köre ugyancsak

k

. Megemlítjük még, hogy

k

érinti az

A B C

háromszögbe beírt kört is, úgyszintén a 3 hozzáírt kört (a háromszög egy oldalát kívülről és két oldalának meghosszabbítását érintő kört). Hozzávéve e 4 érintési pontot, valamint ugyanezeket az

M A B

M B C

M C A

háromszögek részéről, a

k

-n levő nevezetes pontok száma 25-re emelkedik.
Derékszögű háromszögben azonban

M

egybeesik a derékszög csúcsával, ezért a további 3 háromszög elfajult vagy azonos az eredetivel.
Egyenlő szárú háromszögben szintén csökken e nevezetes pontok száma, egyenlő oldalú háromszögben még inkább.