Feladat: 1467. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: -
Füzet: 1974/február, 67 - 69. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Egyenlő szárú háromszögek geometriája, Sokszögek szerkesztése, Szabályos sokszögek geometriája, Alakzatok köré írt kör, Gyakorlat
Hivatkozás(ok):Feladatok: 1973/március: 1467. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Jelöljük az AB egyenesnek a szabályos háromszög köré írt körrel való második metszéspontját N-nel, az egyenlő oldalú háromszög A-val szemközti csúcsát R-rel, a B-vel megfelezett oldal másik végpontját S-sel, az egymással egyenlő BM, AN szakaszok hosszúságát p-vel.

 

 

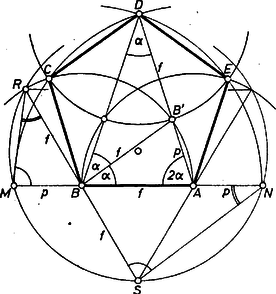1. ábra
 

Az NMR és NSR, valamint az MRS és MNS szögek páronként egyenlők mint ugyanazon íven nyugvó kerületi szögek, ezért a BNS és BRM háromszögek hasonlók, amiből adódik, hogy
(f+p):f=f:p.(1)
Az előírt egyenlő szárú háromszögben AB=f és BD=DA=f+p. Mérjük fel DA-ra a DB'=f szakaszt. Az előző aránypárból és a közös szögből következik, hogy az ABB' háromszög hasonló a BDA háromszöghöz, ABB'∢=BDB'∢=α. Másrészt az ABB' háromszög a hasonlóság miatt szintén egyenlő szárú, tehát AB=BB'=B'D=f. Innen BDB'∢=DBB'∢=α, DBA∢=2α. Eszerint az ABD háromszög szögeinek összege 5α=180∘, ahonnan α=36∘. Tehát az ABD háromszög egy szabályos ötszög két átlója és egy oldala által alkotott háromszög.
Ezek szerint C a B' pont tükörképe BD-re, tehát BCD∢=BB'D∢= =108∘ ‐ és ugyanekkora a DEA∢, hiszen E a C tükörképe a DBA háromszög tengelyére, továbbá CBA∢=CBD∢+DBA∢=B'BD∢+DBA∢=3α=108∘ ‐ és ugyanekkora az EAB∢ , végül a CDE szög is mint a szerkesztett ötszög ötödik szöge. A kérdéses ötszög mindegyik oldala f, mindegyik szöge egyenlő, tehát az ötszög szabályos.
Ezzel a feladat állítását bizonyítottuk.
 

b) Az eredményünkből következő AD=AC=BE egyenlőség miatt az ötszög C csúcsa az A középpontú AD sugarú körön, E pedig a B középpontú ugyanekkora sugarú körön is rajta van. Mivel ezt a két körívet már a D szerkesztésekor megrajzoltuk, ezeket a D középpontú, f sugarú körrel elmetszve egyszerre kapjuk a C és D csúcsok helyzetét. Ezáltal valóban sikerült a szerkesztés puszta végrehajtási lépéseinek számát csökkenteni, elmaradhat a B és A körüli f sugarú körívek megrajzolása.
 

c) Előző bizonyításunk alapján, a szakaszok szerepét megváltoztatva (1) így is olvasható: az f alapon p szárral szerkesztett egyenlő szárú háromszög hasonló az (f+p) alapon f szárral szerkesztett egyenlő szárú háromszöghöz, amilyen az 1. ábrán kapott szabályos ötszög DCE részháromszöge. Eszerint adott AB=f átlójú szabályos ötszög szerkesztése céljára a feladatban leírt szerkesztést az M pont előállításáig változatlanul megismételhetjük. Ezután D az AB alapon BM szárral, C és E pedig a BD, ill. AD alapon ‐ ezeknek AB-t tartalmazó partján ‐ AB szárral szerkesztett egyenlő szárú háromszög csúcsai. Így az ADBEC ötszög átlói egyenlők, és ‐ mint a BAD∢=ABD∢=36∘ szögekből kiindulva a fentiekhez hasonlóan kiszámítható ‐ mindegyik szöge 108∘, tehát az ötszög hasonló az 1. ábra eredményéhez, megfelel a követelményeknek (2. ábra). ‐ Azt is mondhatjuk, hogy a leírt szerkesztésben AM helyett BM-et írva és a "kifelé'' szó helyére a "befelé'' szót, az ABCDE szabályos csillagötszög csúcsait kaptuk az AB szakaszból.
 

 

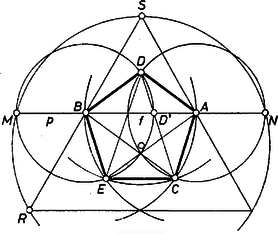2. ábra
 

Eredményünkből látható, hogy C az A körüli, E pedig a B körüli p sugarú körön is rajta van, amelyeket D előállítása céljára már megrajzoltunk, ezért C és E kijelöléséhez az AB sugárral elég D körül kört rajzolni.
Ezzel a feladat megoldását befejeztük.
 

Megjegyzések. 1. A megoldás c) részében leírt szerkesztés helyessége anélkül is bizonyítható, hogy felhasználnánk az a) résznek a szögek értékére vonatkozó eredményeit; illetve ezeket az eredményeket (1)-ből és a c) szerkesztésből is megkaphatjuk. Messe a B körüli, M-en átmenő kör az AB egyenest D'-ben, ekkor AD'=f-p, és mivel (1)-ből
fp=f+pf=1+pfésfp-1=f-pp=pf;(2)
azért a D'AD és DAB háromszög oldalaira
D'ADA=DABA,
a két háromszög hasonló, hiszen A-nál levő szögük közös. Ezért a D'AD háromszög is egyenlő szárú, D'D=D'A, és BAD∢=β jelöléssel ABD∢=ADD'=β, továbbá mivel a BDD' háromszög is egyenlő szárú, azért BDD'∢= =90∘-β/2. Így pedig az ABD háromszög szögeinek összege (90∘-β/2)+3β=90∘+5β/2=180∘, és β=36∘, ADB∢=108∘, BDD'∢=72∘.
Mivel (2) azt is jelenti, hogy a DD'B és DBC egyenlő szárú háromszögekben DD':BD=BD:BC, azért e két háromszög hasonló, CDB∢=BDD'∢, vagyis D'-n átmegy a DC átló. Így pedig C a B pont tükörképe a DD'A szög szögfelezőjére, ami egyben AD felező merőlegese. Továbbá E a C tükörképe AB felező merőlegesére, tehát az ötszög D-nél, A-nál és B-nél levő szöge 108∘, és a C-nél és E-nél levő szögei egyenlők.
2. Sokan az a) rész bizonyítását számítással végezték. (1)-ből
p2+pf-f2=0,pf=-12±52,f+pf=12±52,


és a vagylagos előjelből esetünkben csak a felső használható. Ebből az következik, hogy az egyenlő oldalú és (az utasítás szerint) AB felező merőlegesére tengelyesen szimmetrikus ABCDE ötszög D-ből induló átlóinak és oldalainak aránya (1+5)/2=1,6180. ‐ Másrészt hivatkoztak lapunk F. 1766. feladatára*, hogy ez az arány kétszer akkora, mint a szabályos ötszög szöge felének, 54∘-nak a sinusa. Ebből az következik, hogy az ötszög C és E csúcsánál levő szög 108∘-os. A további három szög értékének megállapítása többnyire hiányzik.
3. Sok dolgozat tartalmazza a beküldő több‐kevesebb ismeretét a folytonos arányú osztásról ‐ klasszikus nevén: szakasz aranymetszéséről ‐, de nem állítja a feladatban kitűzött cél szolgálatába.
*K. M. L. 43 (1971) 14. oldal.