Kezdőlap


Feladat:	1465. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: -
Füzet:	1978/november, 134 - 136. oldal		PDF \| MathML
Témakör(ök):	Érintőnégyszögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/március: 1465. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1.$ Feladatunk olyan kör létezését megmutatni, amely érinti mind a négy ,,új'' közös érintőt. Az iskolai tananyagban arra az esetre láttunk tételt, ha a négy érintő körülzárja a kérdéses kört, az érintési pontok a négyszög oldalszakaszain vannak; ekkor a szemközti oldalpárok összegei egyenlők. Az I. o. tankönyv bizonyítás nélkül kimondja e tétel megfordítását: ha egy konvex négyszög $2 - 2$ szemközti oldalának összege egyenlő, akkor a négyszögbe kör írható. Ennek alapján az 1. ábra esetében elég a szemben fekvő oldalpárok összegének egyenlőségét belátni.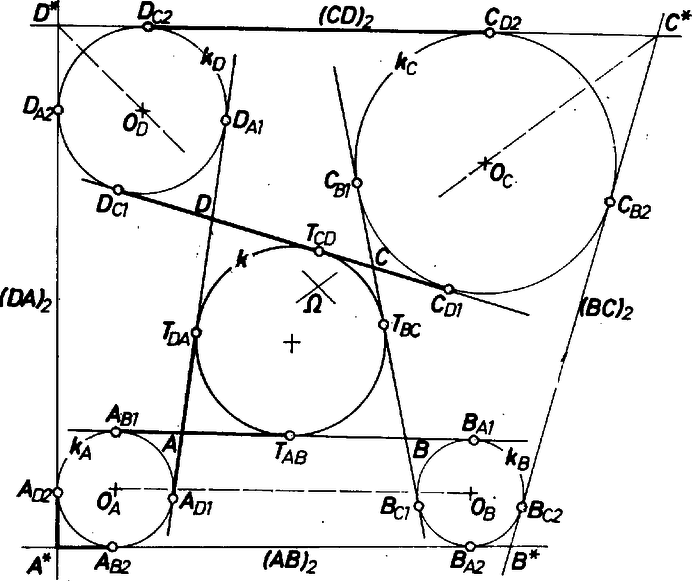

1. ábra

Az eredeti

k

körön és a fölvett

4

körön

4 - 4

érintési pontot kell tekintenünk, együttvéve

20

pontot. Ezeket, valamint az új köröket az alábbiak szerint jelöljük. Az

A B C D = N

négyszög

A B

B C

C D

D A

oldalának érintkezési pontja

k

-val rendre

T_{A B}, ..., T_{D A}

. Az

A

szög csúcsszögtartományában fölvett

k_{A}

kör középpontja

O_{A}

, érintési pontja az

A B

és

A D

oldal meghosszabbításán

A_{B_{1}}

A_{D_{1}}

, és hasonlóan jelöljük a többi három kört, középpontjukat és érintési pontjukat, az

A

B

C

D

betűk helyére ciklikusan a következőt írva, az ábra szerint:

B_{C_{1}}

B_{A_{1}}

C_{D_{1}}

...

D_{C_{1}}

. A

k_{A}

k_{B}

körök második közös külső érintőjét az

A B

egyenesnek az

O_{A} O_{B}

egyenesre való

{(A B)}_{2}

tükörképe adja, érintési pontjai

A_{B_{1}}

-nek és

B_{A_{1}}

-nek a tükörképei:

A_{B_{2}}

, illetve

B_{A_{2}}

, és hasonlóan a további ,,új'' érintők

{(B C)}_{2} = B_{C 2} C_{B_{2}}

...

. Végül a kérdéses négyszög első csúcsa az

{(A B)}_{2}

és

{(D A)}_{2}

tükörképek

A^{*}

metszéspontja, a továbbiak pedig

B^{*}

C^{*}

D^{*}

.
A bizonyításban az

A^{*} B^{*} C^{*} D^{*} = N^{*}

négyszög oldalszakaszait az érintési pontokkal részekre osztjuk. Felhasználjuk, hogy egy pontból egy körhöz húzott két érintőszakasz egyenlő, továbbá, hogy két kör egynemű közös érintőin az érintési pontok közti szakaszok egyenlők. Az utóbbi állítást az új kör párok esetében a külső közös érintőkre alkalmazzuk a végzett szerkesztés utolsó lépéseire, viszont

k

és egy új kör esetében a belső közös érintőkre, a szerkesztés kiindulási lépéseire. Ezek alapján kapjuk, hogy

N^{*}

-ban is egyenlő a két oldalösszeg, tehát az idézett megfordítás szerint

N^{*}

-ba kör írható.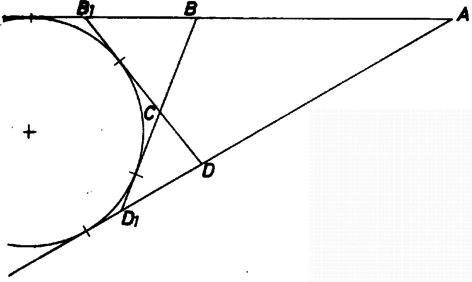

\begin{matrix} A^{*} B^{*} + C^{*} D^{*} & = (A^{*} A_{B_{2}} + A_{B_{2}} B_{A_{2}} + B_{A_{2}} B^{*}) + (C^{*} C_{D_{2}} + C_{D_{2}} D_{C_{2}} + D_{C_{2}} D^{*}) = \\ = A^{*} A_{D_{2}} + A_{B_{1}} B_{A_{1}} + B^{*} B_{C_{2}} + C^{*} C_{B_{2}} + C_{D_{1}} D_{C_{1}} + D_{A_{2}} D^{*} = \\ = A^{*} A_{D_{2}} + A_{B_{1}} T_{A B} + T_{A B} B_{A_{1}} + B^{*} B_{C_{2}} + C_{B_{2}} C^{*} + \\ + C_{D_{1}} T_{C D} + T_{C D} D_{C_{1}} + D_{A_{2}} D^{*} = \\ = A^{*} A_{D_{2}} + A_{D_{1}} T_{D A} + B_{C_{1}} T_{B C} + B^{*} B_{C_{2}} + C_{B_{2}} C^{*} + T_{B C} C_{B_{1}} + \\ + T_{D A} D_{A_{1}} + D_{A_{2}} D^{*} = \end{matrix}

\begin{matrix} (összevonva a2.és7.tagot, valamint a3.és6.tagot, sorrendi cserékkel) \end{matrix}

\begin{matrix} = A^{*} A_{D_{2}} + A_{D_{1}} D_{A_{1}} + D_{A_{2}} D^{*} + B^{*} B_{C_{2}} + B_{C_{1}} C_{B_{1}} + C_{B_{2}} C^{*} = \\ = (A^{*} A_{D_{2}} + A_{D_{2}} D_{A_{2}} + D_{A_{2}} D^{*}) + (B^{*} B_{C_{2}} + B_{C_{2}} C_{B_{2}} + C_{B_{2}} C^{*}) = \\ = A^{*} D^{*} + B^{*} C^{*}, \end{matrix}

ezt akartuk bizonyítani. ‐ A beírt kör középpontját meg is kereshetjük, mint

N^{*}

két szomszédos (belső) szöge felezőinek metszéspontját.

2. ábra

2. Ne hátráljunk meg a feladat megengedte tág lehetőségek elől! Viszont másféle eseteket már csak vázolunk. Tulajdonképpen mindig érintőnégyszögről van szó, ha négy egyenes ugyanazt a kört érinti, és ezek valahogyan négyszöget alkotnak; nem az a lényeges, hogy az érintési pontok az oldalszakaszokon legyenek. A

2.

ábrán a konvex

A B C D

négyszögben és a konkáv

A B_{1} C D_{1}

négyszögben egyaránt a szemben fekvő oldalpárokból képezett különbség abszolút értékei egyenlők,

\begin{matrix} A B - C D = A D - B C, ill. A B_{1} - C D_{1} = A D_{1} - B_{1} C, \end{matrix}

de a kör nincs ,,benne'' egyik négyszögben sem. Gondolhat az olvasó a

B B_{1} D D_{1}

hurkolt négyszögre is! Deltoidnak két érintő köre van, hacsak nem ráadásul még a rombuszság követelményét is teljesíti.
Ha a szerkesztésünkből adódó

N^{*}

négyszögben ezt a tulajdonságot találjuk (az összegek egyenlősége helyett), ezt az

1.

pontban látott elv értelemszerű módosításával ,,bizonyíthatjuk''. (A bizonyítások lényegesebb része azonban mindig a fordított állítás bizonyítása volna!)
3. Mivel a feladat szerint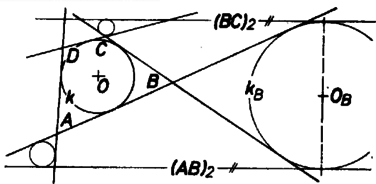

4

kör nagyságát (sugarát) választhatjuk szabadon, könnyű olyan helyzetet létrehozni, amelyben két egymás utáni új közös érintő párhuzamos. Nagyobbra véve

k_{B}

-t, mint amekkora a

k

, található benne olyan átmérő, hogy a végpontjaiban húzott érintők megfelelnek

{(A B)}_{2}

és

{(B C)}_{2}

szerepére, vagyis közrefogják

k

-t és háromszöget metszenek le az

A B C D

négyszög

A

-beli és

C

-beli csúcsszögtartományából. Es ha ezeknek a beírt körét vesszük

k_{A}

k_{C}

szerepére, akkor semmilyen

k_{D}

-vel nem jön létre a kérdéses négyszög (

3.

ábra).

3. ábra