| Feladat: | 1463. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: - |
| Füzet: | 1974/február, 64 - 66. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Részgráfok, Kombinatorikus geometria térben, Kombinatorikai leszámolási problémák, Kombinatorika, Partíciós problémák, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1973/március: 1463. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. a) Ha el tudnánk helyezni hat egész számot egy tetraéder élein úgy, hogy a lapokon az összegük ugyanaz az szám legyen, akkor a hat szám összege páros. Valóban, a lapokon kapott összegek összege egyrészt , másrészt egyenlő az élekre írt hat szám összegének a kétszeresével, hiszen minden él két lapon szerepel. Tehát a számok összege , ahol egész. Az első hat természetes szám összege azonban páratlan, emiatt ezeket nem lehet felírni a tetraéder éleire úgy, hogy a lapokon ugyanazt az összeget kapjuk. Az adott 10 szám közül a tetraéder mindegyik lapja négyet‐négyet nem tartalmaz. Nevezzük az ilyen számnégyeseket a szemben levő csúcs környezetének, összegüket "csúcskörnyéki'' összeg-nek. Nyilván a négy csúcskörnyéki összeg is egyenlő egymással, jelöljük ezt -val, így és mivel az előző egyenletből Ezek alapján felírjuk , és lehetséges értékrendszereit: Próbáljunk olyan elrendezést keresni, melyben . Vegyük 23-nak az adott számok közül a következő négyesből való előállítását a tetraéder felső csúcsának környezete céljára I. 1+6+7+9. Ekkor az alapon levő 3 csúcs környezete céljára 23 további felbontásai közül csak azok jönnek szóba, amelyeknek az I.-vel pontosan egy közös számuk van az egyes alapcsúcsokba lefutó oldalél felezőpontja céljára. Ezek a következők (a közös számot vastag számjeggyel szedtük): Ugyanígy a további három csúcskörnyéki számnégyesnek is páronként egy közös elemüknek kell lennie. Ennek a II.-kal együtt eleget tesz a III. és a VII. a 10-es, ill. 8-as számmal, és ez a két négyes együtt is megfelel, egyetlen közös elemük az 5. Az így adódó elrendezésnek a tetraéder alapsíkjára való merőleges vetületét az 1. ábra mutatja. 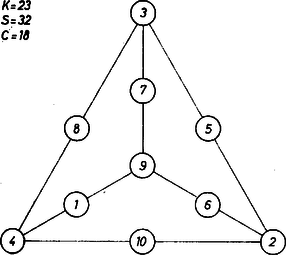 1. ábra A csúcsokba az a száma maradt a számnégyeseknek, amelyik nem közös semelyik másik négyessel sem. Előkészítésünkből hasonlóan kapunk két további megoldást: a II. számnégyest a VIII-kal pótolva, majd abból, a III-at a IV-kel pótolva. II. megoldás. a feladat a) részéhez. Vegyünk egy kitérő élpárt: közülük bármelyiknek a kétszereséhez adjuk is hozzá a másik négy élhez rendelt számok összegét, így két lap számainak összegét, tehát ugyanazt a számot kapjuk. Emiatt a kitérő élekhez rendelt számoknak egyenlőeknek kell lenniük, nem teljesíthető tehát a feladat követelménye. Megjegyzések. 1. A b) rész minden megoldásához van egy komplementer megoldás is, ezt úgy kapjuk, hogy mindegyik szám helyébe az őt 11-re kiegészítő számot írjuk. Nyilvánvaló, hogy ezáltal a csúcskörnyéki összegek, ill. lapösszegek ismét egyenlők lesznek, pl. 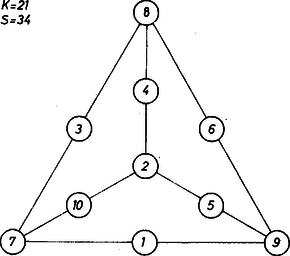 2. ábra 2. Megoldásunkban a 23 négytagú összegre való bontásairól volt szó, különböző természetes számokból. Ha minden szóba jöhető felbontást előállítunk, összesen 16-ot kapunk. Ezekből egy 16‐csúcsú gráfot alakíthatunk ki, ha éllel kötjük össze mindazokat, amelyeknek pontosan egy közös eleme van. Megoldásunkban ennek a gráfnak a négy elemű teljes részgráfjai közül állítottunk elő néhányat, vagyis olyan felbontásnégyeseket kerestünk, amelyekre az teljesül, hogy bennük bármely kettőnek egy közös eleme van (3. ábra). 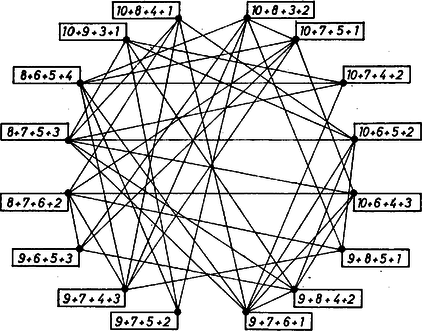 3. ábra |