Kezdőlap


Feladat:	1455. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1974/január, 18 - 20. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos tükrözés, Négyzetek, Négyszögek szerkesztése, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/január: 1455. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a beírt kör középpontját $K$ -val, sugarát $r$ -rel. Az adott kör és az adott egyenes természetesen érintik egymást. Érintse a kör az $A C$ egyenest $E$ pontban, az $A B$ egyenest $F$ -ben (1. ábra).

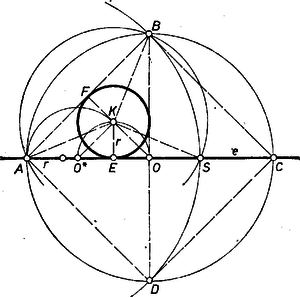1. ábra

A O F

háromszög derékszögű és

A F = F O \cdot K

F O

szakaszon van, ezért

F O = r + K O

A F

egyenlő

A E

-vel, így

\begin{matrix} A E = F O = r + K O, \end{matrix}

(1)

továbbá

K E = E D = r

.
A négyzet

A B

oldalára az előzőek alapján adódik, hogy

\begin{matrix} A B = 2 A F = 2 A E . \end{matrix}

(2)

E

érintési pont helyzetének ismeretében kijelölhetjük a négyzet

O

középpontját is.

E

-ből kiindulva a

K E = r

távolságot két irányba mérhetjük fel az

A C

egyenesre. E két helyzet

K E

-re szimmetrikus, a kapott két megoldás egybevágó lenne, ezért elegendő az egyiknek megfelelően elvégezni a szerkesztést.
Az (1) észrevétel alapján könnyen megszerkeszthetjük a négyzet

A

és

C

csúcsát. Vegyük a

K O

távolságot körzőnyílásba és mérjük fel

E

-ből kiindulva az

A C

egyenesre az

O

-val ellentétes irányba, majd tovább haladva a

K E = r

távolságot is, így megkapjuk az

A

csúcsot.

O

körül

O A

távolsággal leírt körön lesz egyrészt

C

, másrészt a

B

és

D

csúcs is. Ezeket a (2) észrevétel felhasználásával szerkeszthetjük meg:

A

-t tükrözzük

E

-re, képe legyen

S

, a kapott

A S = 2 A E

távolsággal, mint sugárral rajzoljunk kört

A

körül, ez metszi ki a

B

és

D

csúcsokat.
A feladatnak az adott feltételek mellett tehát mindig van megoldása és mint láttuk, lényegében csak egy.

Megjegyzések. 1. A feladat megoldása során az

E

pont helyzetét adottnak tekintettük. A szerkesztés abban az esetben is elvégezhető, ha az érintési pont nincs megadva, annak helyzetét nekünk kell meghatároznunk, szintén csak körző felhasználásával.^{$^{*}$} Ez a következőképpen lehetséges.

K

körül az adott kör sugaránál nagyobb távolsággal kört rajzolunk, ez metszi az adott

e

-t a

P

és

Q

pontban.

P

és

Q

körül

P Q

sugárral köröket rajzolva, a

Q

középpontú kör az

e

egyenest

R

pontban metszi. Ezen metszéspont körül a

P R = 2 P Q

sugárral húzott kör

M

pontban találkozik a

P

középpontú körrel. Végül az

M

középpontú és

M P

sugarú kör kimetszi az

e

egyenesből az

E

érintési pontot (2. ábra).

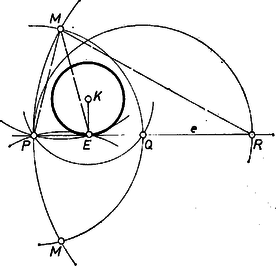2. ábra

A szerkesztés helyességét a következőképpen láthatjuk be. A

P R M

háromszög hasonló

P E M

háromszöghöz. Mindkettő egyenlő szárú, és a

P

csúcsban levő szögük közös. Mivel

M P = P Q

és

P R = 2 P Q

, a hasonlóság aránya,

1 : 2

, ezért

P E : P M = 1 : 2

, megfelelő oldalak, tehát

E

valóban felezi

P Q

-t.
Valamivel nehezíti a feladatot, ha az érintő egyenese helyett annak csak két pontja adott.
2. Némi rövidítést érhetünk el a szerkesztésben a következőkkel (az 1862. feladat^{$^{*}$} II. megoldásához fűzött megjegyzés szellemében).
Az

E A = r + K O

szakasz két tagjából előbb az

r

-et mérjük fel,

O^{*}

végpontját az

O

-val egy csapásra (egy körzőmozdulattal) kaphatjuk, majd

O^{*}

körül az

O^{*} K = K O

sugárral a körző csúcsának fölvétele nélkül kapjuk

A

-t.

S

-et kimetszhetjük az egyenesből a

K

körüli

K A

sugarú körrel is, és ebből: a körből már az

O

körüli

O A

sugarú kör kimetszi a

B

-t, hiszen az értelmezés szerint

K B = K A

^{$^{*}$}A csak körzővel végezhető szerkesztésekkel kapcsolatban lásd Strommer Gyula; Mohr ,,Euclides Danicus''-a c. cikkét K. M. L. 45 (1972) 103-108. old.

^{$^{*}$}Lásd a megoldást K. M. L. 47 (1973) 204-206. oldal.