Feladat:	1454. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1973/október, 70. oldal		PDF  |  MathML
Témakör(ök):	Tengelyes tükrözés, Vetítések, Derékszögű háromszögek geometriája, Körülírt kör, Körülírt kör középpontja, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/január: 1454. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.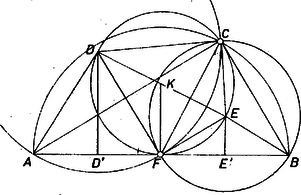   A $D$, $E$ középpontok mindegyike rajta van az $FCA$, $FCB$ háromszögek közös $FC$ oldalának felező merőlegesén, tehát $F$ a $C$ tükörképe $DE$-re mint tengelyre. Másrészt Thalész tétele alapján $F$ az $ABC$ háromszög köré írt kör középpontja, így a $DF$ egyenes az $AC$ oldal felező merőlegese, tehát párhuzamos $BC$-vel. Ugyanígy $EF$ párhuzamos $AC$-vel, az $EFD$ szög váltószöge az $ACB$ derékszögnek, így $DEF$ derékszögű háromszög, a köréje írt $k$ kör $K$ középpontja a $DE$ egyenesen van ‐ felezi a $DE$ átfogót. Így $k$ a látott tükrösség alapján $C$-n is átmegy, ezért azonos az állításbeli körrel. Már csak azt kell belátnunk, hogy $F$ a $k$-nak és $AB$-nek egyetlen közös pontja, $KF$ merőleges $AB$-re. Ez abból adódik, hogy mivel szerkesztésnél fogva $DA=DF$ és $EF=EB$, azért $AB$-re vetítve $D$-t és $E$-t, a $D\text{'}$, $E\text{'}$ pontba, ezek felezik az $AF\mathrm{,}FB$ szakaszt, így pedig a $DE$-t felező $K$ középpont vetülete felezi $D\text{'}E\text{'}$-t, azonos $F$-fel. Ezzel az állítás bizonyítását befejeztük.