Kezdőlap


Feladat:	1453. matematika gyakorlat	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Ács T. , Bagó B. , Balog A. , Baranyi A. , Baranyi J. , Beck L. , Bezdek A. , Csuka Ibolya , Deák L. , Dozmati Z. , Dózsa L. , Forró T. , Gulyás M. , Jakab T. , Jónás B. , Juhász Veronika , Kóczy Annamária , Koltay K. , Maácz Ágnes , Márkus G. , Medvegy M. , Nagy J. , Pecze Z. , Pintér Klára , Seress Á. , Süle G. , Szabó Zs. , Szecsői S. , Szőnyi T. , Torma T. , Vass A.
Füzet:	1973/december, 211 - 212. oldal		PDF \| MathML
Témakör(ök):	Középpontos és egyéb hasonlósági transzformációk, Súlyvonal, Magasságpont, Paralelogrammák, Négyszögek geometriája, Vektorok skaláris szorzata, Gyakorlat
Hivatkozás(ok):	Feladatok: 1973/január: 1453. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Toljuk el az $A C$ szakaszt úgy, hogy $A$ a $D$ -be kerüljön, $C$ új helyzetét jelöljük $F$ -fe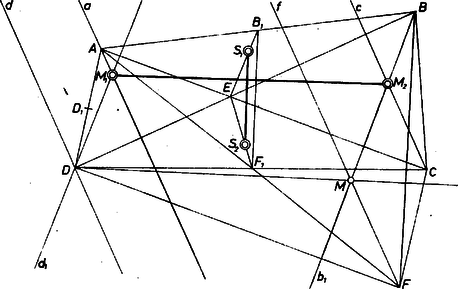l.

Húzzunk az

A

C

D

F

pontokon át a

B D

egyenesre merőleges egyeneseket és jelöljük rendre

a

-val,

c

-vel,

d

-vel és

f

-fel. A

B

és

D

pontokon át az

A C

egyenesre merőlegesen húzott egyeneseket pedig jelöljük

b_{1}

-gyel és

d_{1}

-gyel. Mivel

A D

és

C F

párhuzamosak és egyenlők egymással, az

a

és

d

párhuzamos egyenesek távolsága egyenlő a

c

és

f

távolságával. Emiatt

d_{1}

-nek az

a

és

d

közé eső szakasza egyenlő a

d_{1}

-gyel párhuzamos

b_{1}

-nek

c

és

f

közé eső szakaszával. Jelöljük

a

és

d_{1}

metszéspontját

M_{1}

gyel,

c

és

b_{1}

metszéspontját

M_{2}

vel,

f

és

b_{1}

metszéspontját

M

-mel.
Az elmondottak szerint

D M_{1}

párhuzamos és egyenlő

M M_{2}

-vel, tehát

M_{1} M_{2} ∥ D M

. Mivel

M_{1}

M_{2}

M

rendre a

D E A

B E C

B D F

háromszög magasságpontja (két-két magasságvonaluk metszéspontja), ebből következik, hogy

D M

‐ mint a legutóbbi háromszög harmadik magasságvonala ‐ merőleges

B F

-re. Ezzel bebizonyítottuk, hogy

M_{1} M_{2} ⊥ B F

.
A

B D F

háromszöget az

A

centrumból felére kicsinyítve a

B_{1} D_{1} F_{1}

háromszöget kapjuk, és az itt fellépő

F_{1}

pont egyben a

C D

szakasz felezőpontja, hiszen felezi az

A C F D

paralelogramma másik,

A F

átlóját. A

B_{1} F_{1}

szakaszt az

E

centrumból kétharmadára zsugorítva, új végpontokként az

A B E

C D E

háromszögek

S_{1}

S_{2}

súlypontjait kapjuk, és

S_{1} S_{2} ∥ B_{1} F_{1} ∥ B F

, feladatunk állítását ezzel bebizonyítottuk.

Megjegyzés. Akik ismerik a vektorok skaláris szorzatának fogalmát, azok ennek felhasználásával is bizonyíthatják az állítást.